C. Details of the Model

b. Radiation Scheme

Here, the radiation scheme used in the numerical calculations and the characteristics of the scheme will be described. The key is to discretize the radiative flux equation in two ways and then join the two discretized equations, which allows radiation calculations for a gray atmosphere with an arbitrary optical depth profile.

Finite-Difference Representation of Radiative Flux

Net upward radiative flux for the case of a gray atmosphere is given by the following equation:

$$\begin{eqnarray*} F^{net} (\tau) & = & \pi B(\tau_{top}) e^{-(\tau-\tau_{top})... ...{\tau'} d e^{-(\tau-\tau')} \Deqlab{net rad flux:cont:modify}\end{eqnarray*}$$

where $\tau_{top}$ is optical depth at the top of the atmosphere, thus is $\tau_{top}=0$. πB is equal to σT⁴.

Here, the radiative flux equation is discretized in the same way as in Nakajima et al. (1992), and thus

$$\begin{eqnarray*}\Deqlab{net rad flux:discret} & & F^{net} (k+\frac{1}{2} ) =... ...au_{j+\frac{1}{2}} \geq C_{\Delta \tau} ) \end{array} \right. \end{eqnarray*}$$

Here, K_MAX represents the upper-most layer, and K_MAX = 32 in a typical model calculation. The radiative flux is calculated by joining two sets of discretized equations. Specifically, the integrals for the contributions to net upward radiative flux from optically thin layers and optically thick layers are evaluated using the upper and lower options in the equation, respectively. The fraction of the usage of the upper and lower options in the equation changes according to the value of . If a significantly large value is taken for , the integrals are evaluated entirely with the upper option, which results in a radiative scheme identical to that used in Numaguti and Hayashi (1991).

There exists no that makes the upper and lower options identical. If such hypothetically exists, the relationship

$$\begin{eqnarray*}& & \frac{\pi B(j-\frac{1}{2}) - \pi B(j+\frac{1}{2})} {\tau_... ... } + e^{-(\tau_{k+\frac{1}{2}} - \tau_{j+\frac{1}{2}}) }} { 2 }\end{eqnarray*}$$

needs to hold. Rearranging this condition by letting leads to

$$\frac{1 - e^{\Delta \tau} }{\Delta \tau} = \frac{1 + e^{\Delta \tau} }{2}$$

Unfortunately, no solutions exist for this equation. More accurately, a discontinuity emerges in the evaluated fluxes at the altitude at which the transition between the two options occurs. However, the actual difference between the evaluated fluxes is almost negligibly small. In fact, no evident visible discontinuities exist in the vertical profiles of the radiative flux. (For more information, see Figure 5 of Characteristics of One-Dimensional Radiative-Convective Equilibrium Solutions.)

The above-mentioned complex procedure is necessary because problems arise if either the upper or lower option in the discretized radiative flux equation alone is used. The reasons that the problem arises will be described below, and the values of that are suitable for 3D calculations will be examined.

For the Case of Large C_Δτ

First, the extreme limits are considered in which is set to a significantly large value. This corresponds to using the upper option of the discretized equation for the entire layer, that is, using the radiative scheme of Numaguti and Hayashi (1991). As an example, results will be shown for = 106, Pn0 = 105, and a vertical grid resolution of L1000. The relationship between Tg and OLR from this case is almost identical to that from = 10-1 (not shown). However, the vertical profile of radiative flux at high temperatures is not calculated properly. Figure 1 shows the vertical profile of net upward radiative flux for the case of Tg = 550 K. Unlike in the case of = 10-1, net upward radiative flux increases toward the surface in the layer below the vicinity of log10σ = - 2. Net upward radiative flux decreases from the top to a certain level in the middle layer, and below the level flux increases again. This tendency is attributable to the following reason. If the atmosphere becomes optically thick, only the terms associated with j = k remain in the lower option of the discretized equation, which then leads to for the evaluation of net upward radiative flux. Properly, Fnet should be represented as

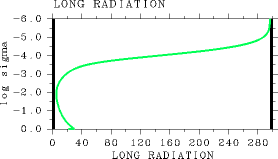
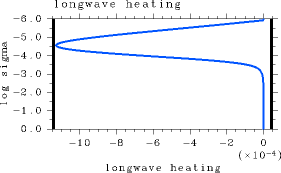
(a) (b) Figure 1: The results for the case of = 106. For L1000, pn0 = 105, and Ts= 550 K. (a) The vertical profile of net upward radiative flux (W/m2). (b) The vertical profile of radiative heating rate (K/sec).

In this example calculation, the values of σT⁴ and net upward radiative flux are

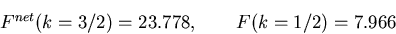
For the case of L32, the above-described phenomenon is more amplified. Net upward radiative flux starts increasing near log10σ = - 3 from higher to lower altitudes, however, it starts decreasing again around log10σ = -1 (Figure 2(a)). This profile results because the net upward radiative flux is determined by σT4k-1 - σT4k below log10σ = -3.0. The decrease in net upward radiative flux from higher to lower altitudes near the surface is attributable to small vertical grid intervals near the surface. The net upward radiative flux values around log10σ = - 1 for the case of = 106 are larger than those for the case of = 10-1 by 400 W/m2. The differences in both upward and downward radiative fluxes in the middle layer between the case of = 106 and the case of = 10-1 are approximately 200 W/m2. On the other hand, the error in the radiative heating profile which is important for time evolution problems in 3D model is relatively small. (Figure 2(b)).

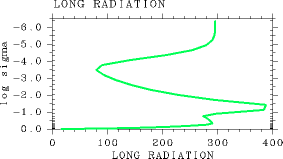
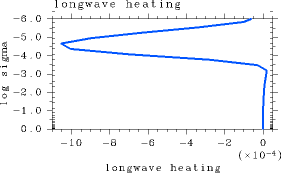
(a) (b) Figure 2: The results for the case of = 106. For L32, pn0 = 105 Pa, and Ts = 550 K. (a) The vertical profile of net upward radiative flux (W/m2). (b) The vertical profile of radiative heating rate (K/sec).

In the case of L32, a discontinuity arises in the middle layer of the vertical profile of radiative flux for ≥ 10.0. Though not shown, in the case of L32, the radiative flux can be calculated with few problems as long as ≤ 1.0.

For the Case of Small C_Δτ

The behaviors of the results from the extreme limit of a significantly small will be examined. The results under consideration correspond to those that are obtained by evaluating radiative flux integrals for the entire layer with the use of the lower option of the discretized equation. As an example, results will be shown for = 0.0, Pn0 = 105, and the vertical grid resolution of L32. When 1D equilibrium solutions for this case are obtained according to the procedure for the 1D convective-radiative equilibrium calculation, the final values of net upward radiative flux appear to be accurate (not shown). However, in the case of Tg = 250 K, the radiation calculation for states in which an adiabatic structure is adopted from the bottom to the top of the atmosphere cannot be accurately performed. Discontinuities arise in the upward and downward radiative flux profiles as shown in Figures 3(a) and 3(b). Incidentally, such discontinuities are clearly present up to approximately Tg = 300 K. The reason is that the value of $$\Deqlab{de/dtau} \Deqlab{de/dTau} \DD{e^{-\tau}}{\tau} \r... ...\frac{1}{2}} )} }{\tau_{j-\frac{1}{2}} - \tau_{j+\frac{1}{2}}}$$ becomes zero in the optically thin layer, that is, in the upper, low-temperature layer. When this option is used, the values of τj-1/2 and τj+1/2 become significantly small. 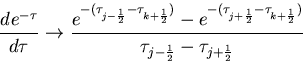For this reason, the calculation yields a numerically equal value for $e^{-(\tau_{j-\frac{1}{2}}-\tau_{k+\frac{1}{2}} )}$ and $e^{-(\tau_{j+\frac{1}{2}}-\tau_{k+\frac{1}{2}} )}$ within the range of numerical error, resulting in zero for the difference between the two terms. 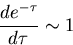Properly, the values of both $d e^{-\tau}$ and $d \tau$ become quite small, leading to $$\DD{e^{-\tau}}{\tau} \sim 1$$ In the layer above the altitude at which becomes zero, the downward radiative flux is determined by $$- \pi B(K_{MAX} + 1) e^{-(\tau_k - \tau_{K_{MAX}+1})} + \pi B(k)$$ is thus smaller than the correct value of downward radiative flux. 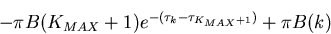Similarly, for the upward radiative flux, some of the additive terms drop away above the altitude at which becomes zero.

(a) 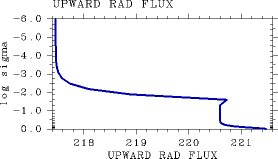(b)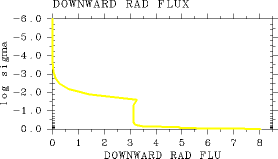 Figure 3: Radiative flux profiles obtained with = 0.0 for a state in which an adiabatic structure is adopted from the bottom to the top of the atmosphere. (a) Vertical profile of upward radiative flux (W/m2). (b) Vertical profile of downward radiative flux (W/m2). For the case of L32, pn0=105 Pa, and Ts= 250 K.

Furthermore, the above-mentioned problem occurs in a more extreme manner with increasing vertical grid resolution. In the case of L1000, the value of OLR can no longer be calculated correctly, and thus an accurate relationship between T_g and OLR cannot be obtained (not shown).

Consequently, the upper option of the discretized equation cannot be applied for the entire atmospheric layer. However, it has been confirmed that radiative flux can be calculated without difficulties for ≥ 10^-7 (not shown).

Summary

If the upper option of the discretized radiative flux equation alone is used, a problem arises in the radiation calculations for an optically thin atmosphere. Furthermore, the lower option of the discretized radiative flux equation alone cannot be used for an optically thick atmosphere. However, a combination of the two options of the discretized equation allows radiation calculations of a gray atmosphere with an arbitrary profile of optical depth. In this regard, the value of C_Δτ that prescribes the switchover between the discretized equations needs to take a value between 1.0 and 10^-7. Based on the results above, a value of 0.1 is adopted for C_Δτ in the present study.

C.b. Radiation Scheme