次の渦度方程式に支配される回転球面上の2次元非圧縮流れを考える.

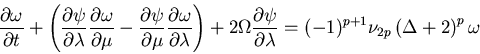
ここで, ψ(λ, μ, t): 流れ関数, ω(λ, μ, t): 渦度の鉛直成分(≡ Δψ), λ: 経度, μ: サイン緯度, t: 時刻, Ω: 球自転角速度, ν_2p: 超粘性係数, p: 超粘性の次数, である. また, Δは 水平ラプラシアンで以下のように定義される.

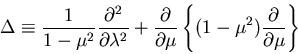
なお,

• 長さの次元は球半径で, 時間の次元はある時間スケール T でそれぞれ 無次元化してある.
• 上の渦度方程式は, 非粘性の場合には, ポテンシャル渦度 q ≡ ω + 2Ωμ のラグランジュ的保存を表わすことになる.
• 渦度方程式右辺の超粘性項は, 数値計算が破綻しないための 便宜的なものである.
• 渦度方程式右辺の超粘性項の (Δ+2) の中の "+2" は全角運動量を 保存させるために付加されている.

従属変数 ψ を球面調和関数で以下のように展開する:

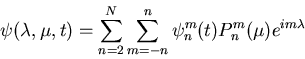
ここで,

• P_n^m(μ)は, 2に正規化されたルジャンドル陪関数 である.
• 展開の n が 2 からスタートしているのは, n = 1 の成分は, 渦度方程式の保存量である全角運動量に対応するため, これを 0に定めて いるからである.

上の展開に基づいて, スペクトルガラーキン法により, 渦度方程式から 展開係数 ψ_n^m(t) に対する連立常微分方程式系を導く. 非線型項は実空間で計算し, フーリエ-ルジャンドル変換で 波数空間に戻す変換法を用いる. エイリアシングを除 くために, N=682 で切断した場合には, 全球面領域を 2048(経度方向)×1024(緯度方向)の変換格子で, N=341 で切断した場合には, 1024×512の変換格子で覆う.

減衰性乱流の実験では, ある初期乱流場を与えて時間発展をみることになる. エネルギー密度は,

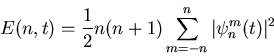
と表わされる. 初期のエネルギースペクトルが Cho and Polvani(1996)の用 いた分布関数,

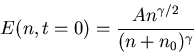
になるように拘束して, 各帯状波数 m 成分の振幅と位相を乱数で与え る. ここで, 係数 A は無次元化した全運動エネルギー: E_total ≡ Σ_n=2^N E(n,t=0) が1となるように定める. n₀ は中心波数 を与えるパラメータで, 10, 50 または 100 とする. また, γ はスペ クトル幅をきめるパラメータで, 大きい値ほど初期エネルギーを狭い波数帯に 限ることになる. 本研究では, 1000 とした.

• E_total = 1 と定めたということは, 逆に言えば, 渦度方程式の無次元化に用いた時間スケールとして (球半径) / √(E_total) を用いたとみなすこともできる.

自転角速度 Ω を実験パラメータとして, 0, 25, 50, 100, 200, 400の6つの値で与え る. Ω≠0の場合には, 惑星は単位時間あたり Ω/(2π) 回 転することになる.

• このスケーリングにおける無次元Ωは, 次元つきの 球半径(a^*), 球自転角速度(Ω^*), 平均的風速 (U^*)に対して, Ω=√2×a^*Ω^*/U^* なる対応関係がある. 本研究で扱っているモデルは2次元非圧縮流体なので, 現実の惑星大気 とは非常にかけ離れてはいるが, あえて対応を考えてみると, 例えば, 地球に関しては, a^*=6.37×10⁶ m, Ω^*=7.29×10^-5 s^-1 であり, U^* として, 15 ms^-1 を使うと, Ω = 43.8 が得られる. また, 木星に関しては, a^*=6.99×10⁷ m, Ω^*=1.76×10^-4 s^-1 であり, U^* として, 50 ms^-1 を使うと, Ω = 348 が得られる. 従って, 本実験で用いたΩをあえて地球および木星と対応づけるならば, Ω = 50 の実験がおおむね地球パラメターに相当し, Ω = 400 の実験がおおむね木星パラメターに相当する実験ということになる.

ここで, 渦度方程式の非線型項が線型の自転効果項と同程度の大きさとなる波数 (Rhinesスケールに対応する波数): n_β≡√(πΩ/(4U))= √(πΩ/(4√(2×E_total)) ) =√(πΩ/(4√2)), が重要な指標となる. 実際, 減衰性乱流の時間発展の様相は, n_βと初期エネルギー ピークの波数n₀との大小関係に大きく依存している. n_β > n₀ ならば, 初期から線型項が非線型項より卓越するので, 必ずしも乱流理論で考 えたエネルギー逆カスケードの状況が出現するわけではない.

数値粘性は, p=8 とし, ν_2p = 1×10^-43 (N = 682のとき); 1×10^-38 (N = 341のとき), で与える. 時間積分には4次精度のルンゲ-クッタ法を用い, 時間刻みは Δt = 5×10^-4 (N = 682のとき), 1×10^-3 (N = 341のとき); として, t=5 まで時間発展を計算する.

なお, 数値計算には, ISPACK(石岡, 1999) 中の効率的変換コードを用いている.

<<index <previous next>