|
B.e. Ground and surface layer
|
Time integration of the 1D thermal conduction equation
(A.55)
in Appendix A.e is performed by the
Crank-Nicolson scheme. Space differencing for Equation
(A.55) is
evaluated by the second-order centered scheme. Ground temperature and
the vertical grid interval are evaluated on the grid point and the
heat flux is evaluated on the half grid point. The number of vertical
grid points is  and the suffix varies,
and the suffix varies,
 ,
from the lowest grid point.
The temperature at highest grid point, ,
from the lowest grid point.
The temperature at highest grid point,
 is assumed to be surface temperature,
is assumed to be surface temperature,
 . .
Where
 .
If the terms at .
If the terms at  are moved to the left-hand side and the terms at
are moved to the left-hand side and the terms at
 are moved to the right-hand side, then
are moved to the right-hand side, then
Where
 .
When .
When
 ,
this equation can be represented in matrix form. ,
this equation can be represented in matrix form.
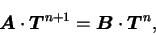 |
(B.61) |
The matrix
 is a J'-th order square matrix and its elements are
represented as follows.
is a J'-th order square matrix and its elements are
represented as follows.
Considering the upper boundary condition
(A.56)
and the insulation lower boundary,
(B.61) can be modified as follows.
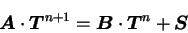 |
(B.62) |
Therefore,
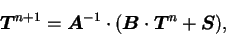 |
(B.63) |
where the first and  th diagonal element of th diagonal element of
 are represented as follows.
are represented as follows.
 is a column vector whose dimension is
is a column vector whose dimension is
 and its elements are represented as follows.
and its elements are represented as follows.
|