| SPMODEL: A Series of Hierarchical Spectral Models for GFD | Index |
When nonlinear terms or linear terms with spatially varied coefficients are included in the governing equations, it is convenient, in programming with SPMODEL library, to apply the transform method to evaluate these terms. The transform method is an evaluation method by converting spectral data of the variables back to grid data in real space, performing multiplication of nonlinear terms or terms with non-uniform coefficients on these grid points, and then converting the results back again into spectral data.
The procedure of transform method can be easily realized with a nesting of the functions of the SPMODEL library. For example, the following advection term and linear term with a non-uniform coefficient,
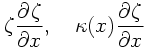
are evaluated with only one statement, respectively:
ĦĦĦĦe_g(g_Zeta*g_e(e_Dx_e(e_Zeta))), e_g(g_Kappa*g_e(e_Dx_e(e_Zeta)))
where g_Kappa is an array data storing the value of κ at each grid point.
When the transformed method is used, the problem of aliasing error should be kept in mind. Insufficient number of grid points in real space where multiplication is performed results in the undesirable intrusion of unwanted high wavenumber components into the required lower wavenumber components, which then gives rise to aliasing errors. To avoid this problem, a larger number of grid points than the degree of the spectral space (or truncation wavenumber) are often prepared according to the order of the nonlinear terms. For example, in the case of a spectral calculation of the second-order nonlinear terms with the Fourier series in a cyclic boundary domain, it is necessary to satisfy an inequality J > 3N, where J and N are the number of grid points in real space and the truncation wavenumber, respectively. Refer to [5] for further detailed explanation.
You should bear in mind that, in exchange for the convenience in programming, the computing efficiency is sacrificed in the resulting program because of large computation time required for the transformation.
| SPMODEL: A Series of Hierarchical Spectral Models for GFD | Index |