| 階層的地球流体スペクトルモデル集 SPMODEL | Index |
支配方程式に非線形項あるいは係数が定数でない線形項が含まれている場合, それらの項を SPMODEL ライブラリを用いてプログラミングするには 変換法を適用するのが簡単で見通しが良い. 変換法とは, 一度変数を実格子点上へ逆変換して非線形項あるいは 非定数線形項の積の計算を行ない, 再びスペクトルデータへと変換して 評価する方法である.
SPMODEL ライブラリを用いると, このような変換操作を 関数のネスティングを行なうことで簡単に実現できる. 例えば移流項と非定数の線形項
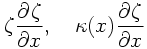
の計算はそれぞれ
e_g(g_Zeta*g_e(e_Dx_e(e_Zeta))), e_g(g_Kappa*g_e(e_Dx_e(e_Zeta)))
という一つの項として書き表せる. ここで g_Kappa は格子点毎のκの値を代入した配列である.
変換法を用いる場合に気をつけるべき点はエイリアスエラーの問題である. 積を実行する実空間の格子点数が十分でないと, 積で生じる高波数成分が 求めたい(低)波数成分にまで混入してしまい誤差が生じる. この対策として, 非線形の次数に応じて波数空間の自由度(切断波数)よりも 多くの格子点を取っておく方法が取られる. 例えば 周期境界条件下のフーリエ級数によるスペクトル計算では, 2 次の非線形項に対しては切断波数 N と格子点数 J を J > 3N を満たすように 選ぶ必要がある. より詳しい解説は[5]を参照されたい.
さらに, プログラミングが簡単である代償として, 場合によっては変換に要する計算時間がかかりすぎ 効率の悪いプログラムとなる可能性があることも 念頭においておく必要があるだろう.
| 階層的地球流体スペクトルモデル集 SPMODEL | Index |