| 階層的地球流体スペクトルモデル集 SPMODEL | << Prev | Index| Next >> |
ここでは spmodel ライブラリを用いたスペクトル法による流体計算の プログラミングの手順を説明する. スペクトル法による流体数値計算の基本的な知識は[5] などを参照していただきたい. 手順は次のようになる.
以下, 例として周期的境界の下での長さ L の 1 次元領域で KdV 方程式の時間発展を計算するためのプログラミングを行なってみる. 支配方程式は
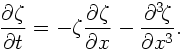
1. 使用するモジュールは 第3節 の例で示した 1次元周期境界条件用のものである.
2. 空間次元 x に関する Forier 変換および逆変換は 次のように定義される.
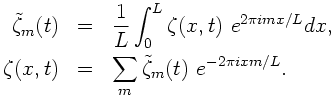
支配方程式を Fourier 変換すると
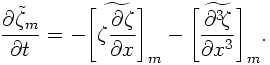
チルダ記号と下付き添字とで Fourier 変換の波数成分を表している.
3. 時間に関して, たとえばオイラー法で差分化すると

ここで, 各項の上付き添字 τ, τ+1 は 現在の時間ステップと次の時間ステップを表している.
4. 以上の定式化から, プログラムの時間積分ループ部分は以下のように書き 下すことができる.
do it=1,nt
e_Zeta = e_Zeta + dt * &
( -e_g(g_e(e_Zeta)*g_e(e_Dx_e(e_zeta))) &
- e_Dx_e(e_Dx_e(e_Dx_e(e_zeta))) )
enddo
非線形項の見積もりには, 実空間へ逆変換した格子点上にて積を計算し再び波数空間へと変換する方法, すなわち, 変換法 を適用している.
プログラムの構築が容易
上の例での 最終的なプログラムの主要部が元々の支配方程式の 数学的形式と対応がついている ことに注意されたい. この点が SPMODEL プログラミングの最大の利点である. スペクトル法による数値計算でありながら, 簡単な支配方程式ならば直接プログラムを書き下すことができる. さらに, 関数の機能と入出力の配列が定義されている空間がわかるよう 関数の名前が統一されているので, マニュアルをあまり見なくてもプログラムを書いていくことができる.
これに対して(例えば FORTRAN77 を使った)従来のスペクトル法による数値計算の プログラミングでは, 波数や成分間の相互作用の形を含んだ各スペクトル成分の式を 書き下す定式化の作業が必要があり, その作業コストが無視できなかった.
プログラムが可読である
プログラムソースコードは元の支配方程式の数学的表現と良く対応している ので, プログラムを理解することが容易である.
対して(例えば FORTRAN77 を使った)従来のスペクトル法による数値計算では, プログラムのために定式化された式が支配方程式から形が変わってしまうので, でき上がったプログラムから支配方程式を読み取ることは困難である.
プログラムの修正や改変も容易である.
上記二つの特徴の結果として容易な修正や改変が可能となっている.
| 階層的地球流体スペクトルモデル集 SPMODEL | << Prev | Index| Next >> |