5.2. 2 次元 2 重周期境界領域でのβ平面順圧モデル

階層的地球流体スペクトルモデル集 SPMODEL << Prev | Index| Next >>

5.2. 2 次元 2 重周期境界領域でのβ平面順圧モデル

2 次元 2 重周期境界領域でのβ平面順圧モデルの支配方程式と境界条件は次のようなものである.

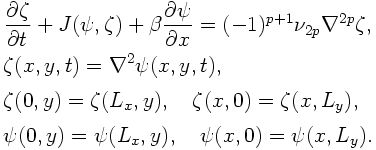
無限領域の場合に, この系にはモドンと呼ばれる孤立渦解が存在する ([8], [9]). その形は渦の中心を原点とする平面極座標 (r,θ) を用いて次のように表される.

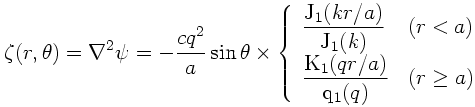
ここで a, c はそれぞれ孤立渦の半径と伝播速度, q = √(β/c), そして k は分散関係に相当する関係式,

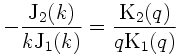
から定まるパラメターである.

これらをプログラミングしたソースコードの全体が plbaro-beta_abcn_test3.f90 である. 支配方程式の時間積分は散逸項を Crank-Nicolson スキームで, それ以外の項を Adams-Bashforth スキームで行なっており, その主要な時間積分計算は

do it=1,nt
    ee_DVorDt = - ee_Jacobian_ee_ee(ee_StrFunc,ee_Vor)  &
                - Beta * ee_Dx_ee(ee_StrFunc)

    ee_Vor = ( (1.0D0 - ee_HVisc*delta_t/2)*ee_Vor    &
              + 3.0D0 * delta_t/2.0D0 * ee_DVorDt  &
              - 1.0D0 * delta_t/2.0D0 * ee_DVorDtB ) &
            /(1.0D0 + ee_HVisc*delta_t/2)

    ee_DVorDtB = ee_DVorDt
    ee_StrFunc = ee_LaplaInv_ee(ee_Vor)
    ...
enddo

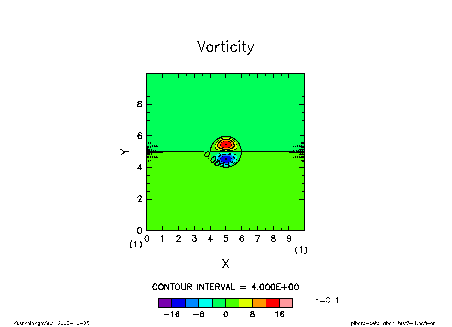
とコードされている. a=c=1 の場合のモドン解を初期値として時間発展させた計算結果を下図に示す. 渦の形が変化せず伝播していく様子が観察できる.

[animation]