5.3. 2 次元チャネル領域でのブシネスク熱対流モデル

階層的地球流体スペクトルモデル集 SPMODEL << Prev | Index| Next >>

5.3. 2 次元チャネル領域でのブシネスク熱対流モデル

温度固定条件の場合

平行平板にはさまれた流体が上下面から一様に冷却・加熱されることにより引き起こされる熱対流のブシネスク流体によるモデルである. 支配方程式は 2 次元のブシネスク流体の渦度方程式と温度の式である.

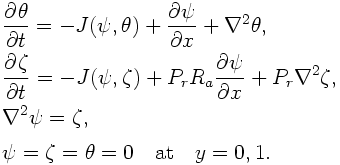
ψは流線関数, ζは渦度であり, θは基本場の温度からの温度擾乱である. 第 1, 2 式の右辺第 1 項の J(ψ,θ), J(ψ,ζ)はヤコビアンであり, 渦度および温度の移流を表している. 第 4 式が上下の境界条件であり, 応力なし(free-slip), 温度固定条件を表している. これらの詳しい定式化と線形安定性に関しては適当な流体力学の教科書 (たとえば[10]) かまたは [11] を参照されたい.

これらをプログラミングしたソースコードの全体が bsncnv-tt-2.f90 である. 境界条件を満たす固有関数系として, x 方向(水平)に通常のフーリエ級数, y 方向(鉛直)にフーリエ sin 級数を選択している. 時間積分の主要部分は以下のとおりである.

do it=1,nt
    es_TempA = es_TempB + &
              dt*( -es_Jacobian_es_es(es_PsiB,es_TempB) &
                    + es_Dx_es(es_PsiB) &
                    + es_Lapla_es(es_TempB) )

    es_ZetaA = es_ZetaB + &
              dt*( - es_Jacobian_es_es(es_PsiB,es_ZetaB) &
                    + Pr*Ra*es_Dx_es(es_TempB) + Pr*es_Lapla_es(es_ZetaB)    )

    es_PsiA = es_LaplaInv_es(es_ZetaA)

    es_TempB = es_TempA
    es_PsiB  = es_PsiA
    es_ZetaB = es_ZetaA
    ...
enddo

接頭子および接尾子 es_, _es は, 1 次元目が通常のフーリエ級数, 2 次元目がフーリエ sin 級数のスペクトルデータであることを表している. 時間積分はオイラー法を適用しており, 最後の文字が B の変数が現在の時間ステップ(Before の省略), A が次の時間ステップであることを表している(After の省略).

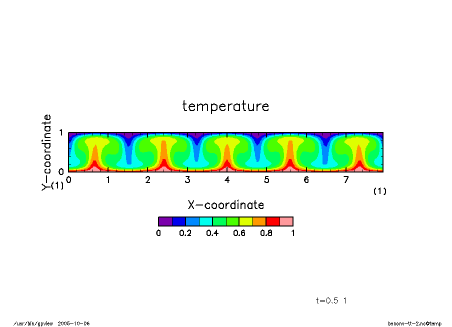
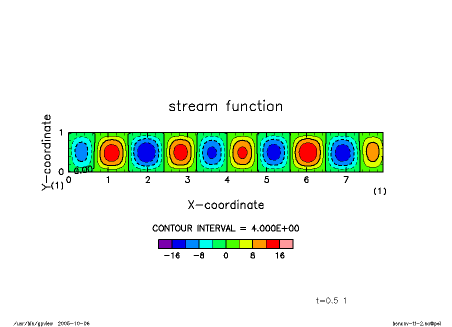
初期条件として温度擾乱に領域中央付近に点擾乱を与えたものから積分した結果を下図に示す. レイリー数R_a, プランドル数P_rはそれぞれ 10000 と 1 である. 縦横比ほぼ 1:1 の対流セルが発達する様子が見て取れる.


[animation]	[animation]

熱フラックス固定条件の場合

境界での熱的条件は熱対流の構造に影響をおよぼすことが知られている ([11]). 上で用いた温度固定条件を熱フラックス固定条件に変更した場合の境界条件は次のようになる.

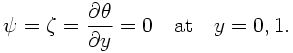
ソースコードの全体は bsncnv-ff-1.f90 である. 熱境界条件を満たすよう温度擾乱は y 方向にはフーリエ cos 級数で展開している. 流線と渦度に関しては温度固定条件の場合と同様に y 方向にフーリエ sin 級数を用いている. 時間積分の主要部分は以下のとおりである.

do it=1,nt
    ec_TempA = ec_TempB + &
            dt*( - ec_Jacobian_es_ec(es_PsiB,ec_TempB) &
                 + ec_yx(yx_es(es_dx_es(es_PsiB)))  &
                 + ec_Lapla_ec(ec_TempB) )

    es_ZetaA = es_ZetaB + &
            dt*( - es_Jacobian_es_es(es_PsiB,es_ZetaB) &
                 + Pr * Ra * es_yx(yx_ec(ec_Dx_ec(ec_TempB))) &
                 + Pr * es_Lapla_es(es_ZetaB)    )

    es_PsiA = es_LaplaInv_es(es_ZetaA)

    ec_TempB = ec_TempA
    es_PsiB  = es_PsiA
    es_ZetaB = es_ZetaA
    ...
enddo

接頭子 "ec_" および接尾子 "_ec" が y 方向にはフーリエ cos 級数展開したスペクトルデータであることを示している. 接頭子 "yx_" および接尾子 "_yx" は 1, 2 次元目がそれぞれ y, x 座標の 2 次元格子点データであることを表している. 流れ場と温度場でスペクトル展開関数が異なるために, 一度実空間格子点データにもどしてからスペクトル展開関数の変換を行なっている.

温度固定条件の場合とおなじ初期値とパラメターを与えて計算した結果が下図である. [11] に詳述されているように, 初期には縦横比 1 程度の対流セルが不安定となって発達するが, 横長の対流セルが最終的に出現し領域を支配する様子が見てとれる.


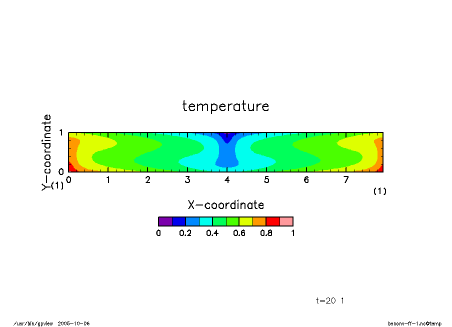
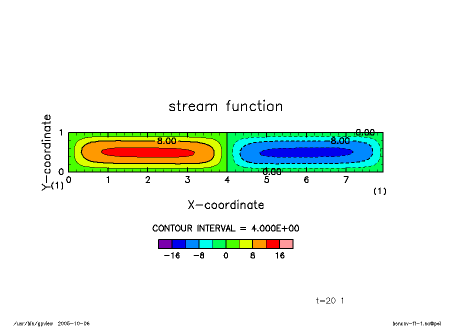
[animation]	[animation]