5.4. 2 次元回転球面上での浅水モデル

階層的地球流体スペクトルモデル集 SPMODEL << Prev | Index| Next >>

5.4. 2 次元回転球面上での浅水モデル

以下は回転球面上の浅水系を用いて山岳に対する大気の応答を研究した [12]の計算を再現するものである. ここでは理想的な山岳応答として計算された, 緯度 30 度, 経度 180 度を中心とする半径 45 度の局所的な山に対して剛体回転分布の西風(東向きの流れ)を与えたときに引き起こされる地球規模な波の伝播を示す.

支配方程式は回転系での線形化した球面上の浅水モデルである.

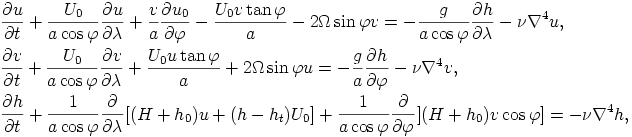
ここでU₀が基本場として与える経度方向の流れ(剛体回転), u,vが速度場擾乱, H,h,h_tが流体層の平均の厚さ, 表面変位および底面地形の高さを表す. Ωは系の回転角速度, νは 4 次のラプラシアンの超粘性係数である. a は球の半径, λ,φが経度・緯度座標を表す.

これらをプログラミングしたソースコードの全体が spshallow_topo_linear.f90 である. 領域が全球面なので, 球面調和函数をスペクトル計算の展開函数系として用いる. このとき支配方程式に対応するプログラムの主要部は次のようになる.

do it=1,nt
    w_U = ( w_U &
        + dt * w_xy( - xy_U0 * xy_GradLon_w(w_U) / R0   &
                     - xy_V  * xy_GradLat_w(w_U0) / R0  &
                     + xy_U0 * xy_V * tan(xy_Lat) / R0  &
                     + 2 * Omega * sin(xy_Lat) * xy_V   &
                     - Grav * xy_GradLon_w(w_H)/ R0   ) &
                     )/(1+Nu*(-rn(:,1)/R0**2)**(ndiff/2)*dt)

    xy_U = xy_w(w_U)

    w_V = ( w_V &
        + dt * w_xy( - xy_U0 * xy_GradLon_w(w_V) / R0   &
                     - xy_U * xy_U0 * tan(xy_Lat) / R0  &
                     - xy_U0 * xy_U * tan(xy_Lat) / R0  &
                     - 2 * Omega * sin(xy_Lat) * xy_U   &
                     - Grav * xy_GradLat_w(w_H) / R0 )  &
                     )/(1+Nu*(-rn(:,1)/r0**2)**(ndiff/2)*dt)

    xy_V = xy_w(w_V)

    w_H = ( w_H &
        + dt * ( - w_Div_xy_xy( xy_U*(H0+xy_H0)+xy_U0*(xy_H-xy_Htopo),   &
                                xy_V*(H0+xy_H0) ) / R0      ) &
                )/(1+Nu*(-rn(:,1)/R0**2)**(ndiff/2)*dt)

    xy_H = xy_w(w_H)
    ...
enddo

接頭子 "w_" および接尾子 "_w" が球面調和函数で展開されたスペクトルデータ, "xy_", "_xy" が 1,2 次元がそれぞれ経度・緯度座標の格子点データであることを表している. 時間積分に関しては, 粘性項は陰解法, その他は陽解法(オイラースキーム)を適用している. -rn(:,1)はラプラシアンを作用させたときにかかる全波数 n(n+1) が格納された配列である.

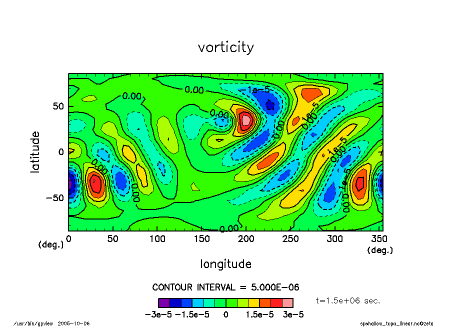
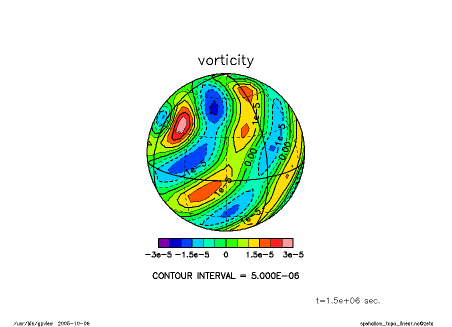
下図は渦度擾乱の分布の時間発展を, 二種類の地図投影で, 示している. 擾乱がロスビー波として大円上に沿って伝播していく様子が見てとれる.


[animation]	[animation]