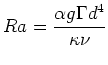古川 & 新野(2006)[4]と同様に、鉛直の回転軸まわりに角速度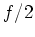 で回転する系におけるブシネスク流体を考える。鉛直方向の深さ、動粘性係数、および上下境界での浮力差によって無次元化された基礎方程式は以下のように書ける。
で回転する系におけるブシネスク流体を考える。鉛直方向の深さ、動粘性係数、および上下境界での浮力差によって無次元化された基礎方程式は以下のように書ける。
ここに、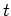 : 時刻、
: 時刻、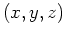 : 空間のデカルト座標(
: 空間のデカルト座標(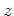 : 鉛直)、
: 鉛直)、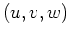 :
: 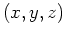 方向の流速、
方向の流速、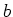 : 浮力、
: 浮力、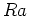 : レイリー数、
: レイリー数、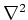 : ラプラシアン、である。なお本研究では古川 & 新野(2006)[4]に倣い、プラントル数を1としている。また、
: ラプラシアン、である。なお本研究では古川 & 新野(2006)[4]に倣い、プラントル数を1としている。また、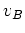 は後述する基本流である1。
は後述する基本流である1。
ここで、次元つきパラメータとの対応について補足しておく。熱膨張率を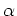 、重力加速度を
、重力加速度を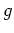 、動粘性係数を
、動粘性係数を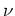 、熱伝導率を
、熱伝導率を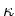 、鉛直方向の深さを
、鉛直方向の深さを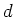 、(下端,上端)の温度を
、(下端,上端)の温度を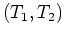 、温度減率を
、温度減率を
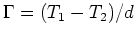 、とすると、
、とすると、
である。無次元化された浮力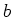 と温度
と温度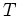 との間には
との間には
の関係がある。3章以降で示す図においては、浮力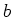 の代わりに温度
の代わりに温度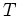 を表示している。ただし、そこでは
を表示している。ただし、そこでは
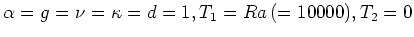 としている。
としている。
SAITO Naoaki
2008-03-07
![]() 、重力加速度を
、重力加速度を![]() 、動粘性係数を
、動粘性係数を![]() 、熱伝導率を
、熱伝導率を![]() 、鉛直方向の深さを
、鉛直方向の深さを![]() 、(下端,上端)の温度を
、(下端,上端)の温度を![]() 、温度減率を
、温度減率を
![]() 、とすると、
、とすると、