| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |
The dependences of mean specific heat on temperature and composition are not considered in our model, since we adopt potential temperature as one of the prognostic variables. The adoption of the value of H2 specific heat at the standard temperature (T = 298.15 K) results in an error of 20 % in adiabatic lapse rate near the NH3 condensation level. However, for the purpose of making a qualitative examination of the structure of the cloud convection layer in Jupiter's atmosphere, the effect of the ignored dependences may be regarded as being insignificant if the resulting error of static stability N2 in the cloud layer is small.
N2 is evaluated in the same way as Sugiyama et al. (2006) [7] once the vertical profiles of temperature and mean mole weight are known.
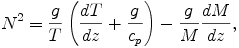
where T is temperature, g is the acceleration due to gravity, M is mean molecular weight, and cp is mean specific heat at constant pressure.
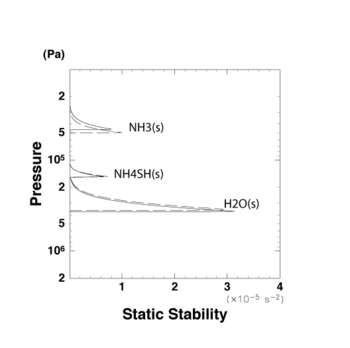
Fig. G.1 shows the vertical profiles of N2 estimated by assuming that dT/dz and dM/dz are those of the pseudo moist adiabatic profiles. The solid line in Fig. G.1 is the results of calculations using the thermodynamic subroutine in the present cloud convection model, and the broken line is the result of Sugiyama et al. (2006) [7] which takes into account the dependences of mean specific heat on temperature and composition.
Fig. G.1 shows that the altitude of stable layers and the peak values of N2 are nearly the same in these two cases. Therefore, for the present purpose, it may be concluded that the effect of the ignored dependences are small.
|
|
Figure G.1: The vertical profile of static stability. The abundances of species are assumed to be the same as the solar abundance [9]. The solid line is obtained when the specific heat is kept constant and the broken line is the result of a more accurate calculation [7]. |
| Development of a Numerical Model for Jupiter's Atmosphere | << Prev | Index| Next >> |