| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |
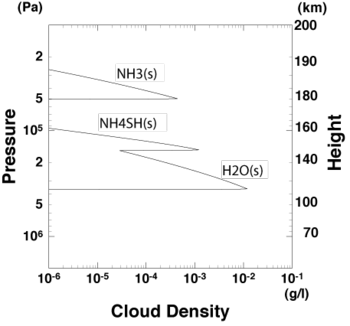
Three cloud layers associated with convective motion are expected to exist in Jupiter's atmosphere: the topmost NH3 ice layer, the middle solid NH4SH layer, and the bottommost H2O ice layer[3],[4] (see Fig. 1.1). Although this cloud structure has widely been interpreted to be the standard structure of Jupiter's atmosphere, it has been estimated using one-dimensional thermodynamical equilibrium calculations in which adiabatic ascent of air parcel and its thermodynamic equilibrium are supposed. Neither convective motion such as advection process nor cloud microphysics such as precipitation of raindrops has been considered in their calculations.
While the formation and dissipation of clouds are affected by convective motion and cloud microphysics, the formation and dissipation of clouds also influence convective motion in return since the stratified structure of the atmosphere is determined by them. Among the previous studies, it was Nakajima et al. (2000)[6] that explicitly considered the formation and dissipation of clouds and convective motion, and discussed the relationship between them. They focused on the effect of H2O condensation, performed a long-time numerical simulation using a two-dimensional convection model that incorporates phase change and cloud microphysics (referred to as "cloud convection model" hereafter), and investigated the characteristics of convective motion and vertical profiles of temperature, clouds, and vapor in a statistical equilibrium state. They showed that the stable layer associated with H2O condensation forms a stable layer which acts as a boundary against convective motion, and which vertically separates the convective layer. Stable layers are also expected to be formed in association with NH3 condensation and NH4SH production reaction which were not considered in Nakajima et al. (2000) [6]. Based on one-dimensional thermodynamical equilibrium calculation [7], the strength of such stable layers were estimated to be of the same order of magnitude as that associated with H2O condensation. Separation of convective motion similar to that associated with H2O condensation might also develop at the bottoms of the other two cloud layers and affect mean vertical clouds structure.
With those backgrounds, here we develop a cloud convection model which incorporates all of the major condensible species in order to enable us to investigate the vertical profiles of clouds and characteristics of circulations associated with them by explicitly resolving convective motion in Jupiter's atmosphere. Since large computational domain and long integration time are needed to acquire and observe a statistically equilibrium state, the convective motion is restricted to be two-dimensional as is in Nakajima et al. (2000)[6], while the quasi-compressible system [1] is utilized as the basic system for describing fluid motion rather than the anelastic system adopted by Nakajima et al. (2000)[6] to let us free from solving the elliptic differential equation which is computationally expensive when the model domain is large or especially when the model is extended to be three-dimensional. The quasi-compressible system is one of the standard frameworks of the recent cloud convection models for the Earth's atmosphere, since it is a useful approximate system which, compared to the full-compressible system, can suppress the increase of computational cost [8] by substituting the value of sound wave speed to that for the basic reference state. The purpose of the present study is to realize an application of the quasi-compressible system to the Jupiter's atmosphere. In the followings, Section 2 will give a summary on the formulation and the discretization of the model and the visualization technique suitable for presentation of multi-components clouds. In Section 3, we show the result of a long-time numerical simulation of cloud convection in Jupiter's atmosphere carried out as a test run of the developed model. In this simulation, the model atmosphere is subjected to thermal forcing as a rough proxy for both radiative cooling near the tropopause and heating supplied by the convection of deep atmosphere. In Section 4, we give the summary.

Figure 1.1: Vertical profiles of cloud density in Jupiter's atmosphere obtained by one-dimensional thermal equilibrium model. The solar abundances [9] are adapted for the abundances of condensible elements relative to hydrogen. Altitude calculated by hydrostatic balance is also shown. Zero altitude is set at the 30-bar level. This calculation is performed using the numerical code [10] developed by Sugiyama et al. (2006) [7].
| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |