Space discretization

We have chosen the spatially staggered mesh shown in Fig. 2.2. Arakawa-C grid ^[11] is employed for horizontal direction and Lorentz grid ^[12] is employed for vertical direction. Thus, all scalar variables, such as the exner function π, potential temperature deviation θ, and mixing ratios of condensible species q are defined at a common point, and the velocity components are displaced by half a grid. The space derivatives are approximated by the fourth-order centered difference scheme for advection terms and the second-order centered difference scheme for the other terms.

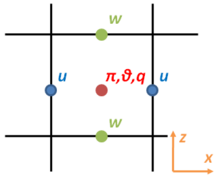
Figure 2.2: Schematic view of grid structure.

Time integration method

Since the quasi-compressible system contains the acoustic mode in their solutions, the time step is severely restricted by the CFL condition for the phase speed of sound waves in the case a simple explicit time integration scheme is used. In order to save computational resources, the acoustic mode is integrated with a short time step and the other modes are integrated with a long time step (time-splitting method; see Fig. 2.3. The acoustic mode is treated by the HE-VI scheme ^[1]. The horizontal propagation of sound waves is treated explicitly (Euler scheme) and the vertical propagation is treated implicitly (Crank-Nicolson scheme). The other modes are treated by the leap-frog scheme with Asselin time filter ^[13]. The coefficient of Asselin time filter is 0.1. Artificial viscosity terms are introduced for the sake of calculation stability (see Appendix D).