空間方向の離散化

格子点は図 2.2 に示すような交互格子を用いる. 変数の配置方法として, 水平方向に荒川 C グリッド ^[11], 鉛直方向にはローレンツグリッド ^[12] を用いる. すなわち, すべてのスカラー量 (エクスナー関数 π, 温位偏差 θ, 凝結成分の混合比 q) を格子の中心に配置し, ベクトル量 (速度 u, w) は中心から半格子ずらして配置する. 移流項に関しては 4 次精度中心差分を用いて離散化し, その他の項に関しては 2 次精度中心差分を用いて離散化する.

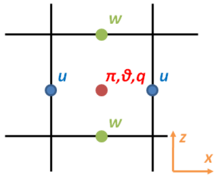
図 2.2: 格子点配置の概念図

時間積分法

準圧縮系モデルは解に音波モードを含むため, 単純に陽的な時間積分法を用いた場合, その時間ステップは音速に対する CFL 条件で規定されてしまう. 計算資源を節約するために, 音波モードを短い時間ステップで積分し, それ以外のモードを長いタイムステップで計算する (モード別時間分割法; 図 2.3). 音波モードは HE-VI 法 ^[1] を用いて数値積分する. この方法では水平方向の音波の伝播は陽的に解き (オイラースキーム), 鉛直方向の伝播は陰的に解く (クランク・ニコルソンスキーム). 音波以外のモードに関しては, リープフロッグスキームに アセリンの時間フィルタ ^[13] を併用して数値積分する. アセリンの時間フィルタの係数は 0.1 とする. また計算の安定性のために, 人工的な粘性項を追加する (詳細は補遺 D).