C. Details of the Model

e. Moist Convective Adjustment Scheme

The treatment of moist convection in ordinary atmospheric GCMs involves an approximation that the water vapor content of the atmosphere is small. However, when the value of solar constant increases, the water vapor content in the atmosphere increases significantly. Therefore, it is not appropriate to use this approximation in this case. In the present study, we adopt a convective adjustment scheme that does not include the approximation that the atmospheric water vapor content is small. The details of this convective adjustment scheme will be described below.

The Adiabatic Equation

The adiabatic condition for air parcels consisting of water vapor and dry air can be expressed as

If this equation is discretized for the case of c_pn=c_pv, which is the case under consideration in the present study, the discretized form of the adiabatic equation

$$B \cdot \Delta T_{k-1} + C \cdot \Delta T_{k} = ST$$

is obtained. Here,

where

Using the discretized adiabatic equation above, the temperature structure in the 1D model is determined and the moist convection adjustment scheme is constructed.

Method for Constructing an Adiabat in the One-Dimensional Model

To obtain an adiabatic structure in the 1D model, T_k and q_k = q^*(T_k) are determined starting from the bottom with T_g and q^*(T_g) up to the upper-most layer in such a way as to fulfill the adiabatic equation. In practice, with given T_k-1 and q_k-1 , an arbitrary initial estimate value is assigned to T_k and the deviation from the actual T_k is evaluated from

$$\Delta T_{k} = \frac{ST}{C}$$

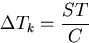
in order to determine T_k. Then, q^*_k is determined from the saturated vapor pressure curve.

Moist Convective Adjustment Scheme

In the 3D calculations, the temperature and water vapor profiles are adjusted to the profiles that are determined by the moist adiabat at points meeting the following conditions:

1. 1.unstably stratified
2. 2.saturated or supersaturated

In the course of the adjustment, in addition to the adiabatic conditions, conditions for the conservation of moist static energy between the pre- and post-adjustments

$$\sum \Delta (c_{pd} T_k + L q_k)= 0.$$

will be used. Discretization of this equation leads to a discretized form of the conservation equation for moist static energy:

$$\Delta T_{k-1} = \alpha \Delta T_k + \beta$$

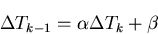
Here

$$\begin{eqnarray*} \alpha & = & - \frac{1 + \gamma_k}{1+\gamma_{k-1}} \frac{\Del... ..._{k-1}} \frac{L}{C_p} \Delta \hat{Q} \frac{1}{\Delta p_{k-1}}.\end{eqnarray*}$$

where

$$\begin{eqnarray*} \Delta \hat{Q} & \equiv & \Delta p_{k-1} (q_{k-1} - q^*(T_{k-... ...\equiv \left. \frac{L}{c_p} \DP{q^{\ast}}{T} \right\vert _{k-1}.\end{eqnarray*}$$

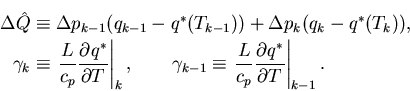
By substituting the discretized conservation equation for moist static energy into the discretized adiabatic equation, the following equation can be obtained:

$$\Deqlab{delta T(k)} \Delta T_k = \frac{ST - \beta B}{C + \alpha B}$$

From this equation and the discretized conservation equation for moist static energy, Δ T_k-1 and Δ T_k are obtained, which are then used to determine the specific humidity as

$$\begin{eqnarray*} q_{k-1} & = & q^*(T_{k-1} + \Delta T_{k-1}), \\ q_{k} & = & q^*(T_{k} + \Delta T_{k})\end{eqnarray*}$$

The adjustments above are made in each layer in order starting at the lowest layer and repeated up to ten times.

C.e. Moist Convective Adjustment Scheme