C. Details of the Model

a. Basic Equations

For the basic equations, a 3D spherical primitive system is used (refer to Numaguti and Hayashi, 1991, and Numaguti, 1992, for details). For the horizontal and vertical directions, a latitude and longitude coordinate (λ, φ) system and a σ-coordinate system are adopted, respectively. The equations of motion, the continuity equation, the hydrostatic equation, the equation of water vapor, the thermodynamic equation, and the surface energy balance equation are as follows:

       

where

$$\begin{eqnarray*} \DD{}{t} & \equiv & \DP{}{t} + \frac{u}{a \cos \varphi} \DP{... ...\DP{}{\sigma} \\ \Phi & \equiv & gz, \\ \pi & \equiv & \ln p_s.\end{eqnarr ay*}$$

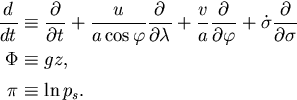
u, v are horizontal wind velocities, is vertical wind velocity in σ-coordinates, T is temperature, q is specific humidity, p_s is surface air pressure, T_g is surface temperature, $\Phi$ is geopotential, f is the Coriolis parameter, a is the radius of a planet, g is the gravitational acceleration, R is the gas constant of the atmosphere, c_p is specific heat at constant pressure, and L s the latent heat of water vapor. $F^{diff}_{\lambda}$, $F^{diff}_{\varphi}$, $F^{diff}_{T}$, and $F^{diff}_{q}$ are horizontal diffusion terms and F_u^vdf, F_v^vdf, F_T^vdf, F_q^vdf are vertical diffusion flux terms. S_q^cond is the specific humidity source term associated with condensation, C_g is the specific heat of the surface, which is set to 0 in practice. q_rad, q_vdfT, and q_vdfq are net radiative flux, sensible heat flux, and latent heat flux terms, respectively.

Table 1 shows the values that are used for the parameters in the model. The value of the water vapor absorption coefficient, $\kappa_v$, was determined using that at 1000 cm^-1 in Figure 2 of Yamamoto (1952). The values of L and p₀^* are set identical to those in Nakajima et al. (1992).

Physical constants
Universal gas constant			R* = 8.314 J mol-1 K-1
Gravitational acceleration			g = 9.8 m s-2
Stefan-Boltzman constant			σ = 5.67 × 108 W m-2 K-4

Model parameters
Molecular weight of dry air		mn = 18 × 10-3 kg mol-1
Molecular weight of water vapor		mv = 18 × 10-3 kg mol-1
Gas constant of dry air		Rn = 461.9 J kg-1 K-1
Gas constant of water vapor		Rv = 461.9 J kg-1 K-1
Specific heat of dry air at constant pressure		cpn = 4Rn = 1616.6 J kg-1 K-1
Specific heat of water vapor at constant pressure		cpv = 4Rv = 1616.6 J kg-1 K-1
Latent heat of water vapor		L = 2.4253 × 106 J kg-1
Constant used in the saturated water vapor pressure equation		p0* = 1.4 × 1011 Pa
Mass of the non-condensable constituents in the atmosphere		pn0 = 105 Pa
Water vapor absorption coefficient		κv = 0.01 m2 Kg-1
Dry air absorption coefficient		κn = 0.0 m2 Kg-1
Radius of planet		a = 6.37 × 106 m

Table 1:Values of various constants and parameters used in model calculations.

It is assumed that saturated water vapor pressure can be given by

$$p_v^{\ast}(T) = p^{\ast}_0 \exp \left( - \frac{L}{RT} \right)$$

as in Nakajima et al. (1992).

C.a. Basic Equations