3.2 Other Details
The following practical procedures have the basis on Dritschel(1989).< Node redistribution >
The nodes on the contour are distributed with a uniform interval initially, but the distribution becomes non-uniform after some time, which gives rise to large error in the calculation of the velocity field, and which requires more calculation time due to unnecessarily crowded nodes.
Therefore, the nodes should be redistributed adequately with a finite time interval.
First, the node density ri is defined using
the curvature ki at the node xi ,
which is the curvature of the circle including three points
xi-1 , xi , xi+1 :
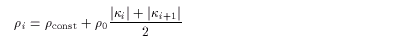 (3.4)
(3.4)
The node xi is fixed as a corner
if the angle of
xi-1 , xi , xi+1
is under 90 degrees.
( The first node is fixed anyway ).
And the nodes are redistributed on the contour between two corners,
called a contour segment.
The number of the nodes n' in the segment is determined with ri;
 (3.5)
(3.5)
where [ ] is Gauss' notation.
Next, i and p , which satisfy the following equation, are sought.
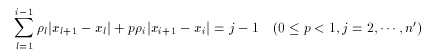 (3.6)
(3.6)
The position of the new node xj is
x(p) , which is located between old nodes
xi and xi+1.
Note that the form of x(p) is determined by the interpolation
using a cubic spline.
< Interpolation >
The contour between adjacent nodes
xi and xi+1
is interpolated using a cubic spline.
 (3.7)
(3.7)
where,
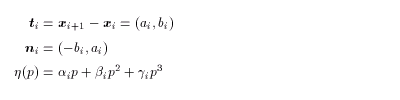 (3.8)
(3.8)
Here, the interpolation coefficients ai,bi,
and gi are given by the curvature ki as follows;
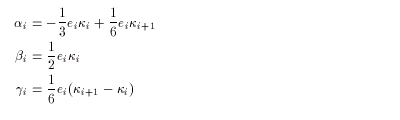 (3.9)
(3.9)
where ki and ei are as follows:
 (3.10)
(3.10)
Note that the continuity of x and ki is assumed
at the points xi and xi+1 .