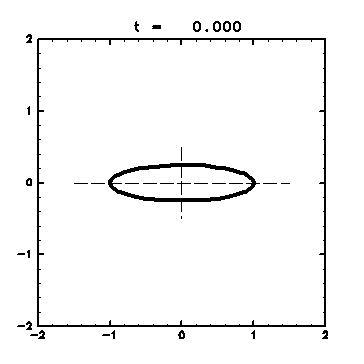
4.1 Time Evolution of an Unstable Elliptical Vortex
4.2 Analysis on the Streamfunction
4.3 Visualization with Passive Contours
4.4 Finite-Time Lyapunov Analysis on Fluid Deformation
4.5 Check by Passive Contour Advection

4.1 Time Evolution of an Unstable Elliptical Vortex

Time evolution of an elliptical vortex patch with a small perturbation is calculated. The time evolution depends on the oblateness of the ellipse and the wavenumber of the perturbation ( Horii,1997 ).

The initial contour shape is
(4.1)
inside of which the vorticity is constant q = 2π , and outside of which q = 0. This type of elliptical vortex rotates with a constant angular velocity g= 2pl/ ( 1 +l )², depending on the ratio of the major axis to the minor axis l ( Lamb,1932 ).

A small perturbation is added to the elliptical vortex in the form ( Dritschel,1989 ):
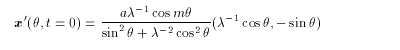(4.2)
In the case of m = 3 , the elliptical vortex is unstable when l > 3 ( Love,1893 ).

The parameters used in the present case study are as follows: Ratio of the major axis to the minor axis: l= 4 Time incriment: Δt = 0.1 Constant part of the node density: rconst = 4.0 Proportional coefficient of the node density: r0 = 4.0 Wavenumber of the perturbation: m = 3 Amplitude of the perturbation: a = 0.005 Animation 1: Time evolution of elliptical vortex (GIF animation; 351kB). The contour position is displayed with a thick line from t = 0.0 to t = 14.0 at an interval of 0.1 . Dashed lines are the directions of the axes of the ellipse in the case of no perturbation. ・ Until t = 5.0 , the vortex keeps its shape and rotates with a nearly constant angular velocity g . ・ After that, the ellipstical vortex is deformed gradually with the developing perturbation. A part of the vortex patch is put out from one edge and is elongated thinner and thinner. This part is called a streamer. Interpreting the situation by the breaking of the wave trapped on the contour, this is similar to the breaking pattern of the planetary waves in the stratosphere in winter ( McIntyre and Palmer,1983 ). ・ As the time goes on, the streamer gets longer and thinner, and surrouds the vortex. The main vortex comes close to a circle in its shape and increases its angular velocity ( cf. (2.13) ).

<<index <previous next>