|
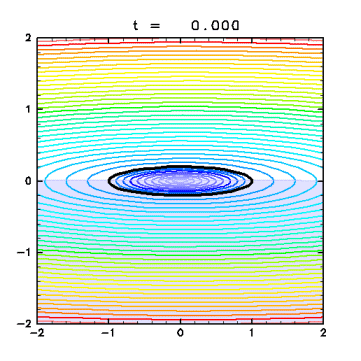
To examine the motion of the fluid where the vorticity jump does not exist,
passive contours are advected to get intuitive images
on the advection and mixing.
Since the velocity at an arbitrary point u( x,y,t ) can be obtained by (2.11), contours put on anywhere can be advected by same numerical method without affecting on the velocity field.
Animation 2:
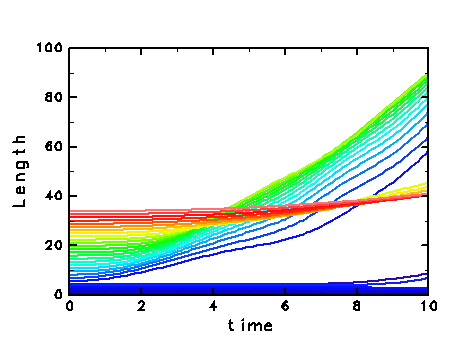
Advection of passive contours (GIF animation; 1990kB). - Passive contours clearly show the flow in other regions than the patch contour where little interest was put on in the previous analyses. - The fluid are deformed even while the elliptical vortex keeps its shape. Especially at the edge of the ellipse, the fluid outside the vortex is dragged and stretched out. - Fluid particles are stretched near the sreamlines containing the stagnation points in the co-rotating frame analyzed in section 4.2 . - A complex flow pattern is produced after the streamer formation. There are many indications of stretching and folding. - This stretching is also recognized as the time evolution of the length of each passive contour. ( Note that the area between two contours is preserved due to the nondivergent fluid. )
- The contours inside the vortex are hardly stretched out. - The contours a little outside are stretched at an almost constant rate in the early phase. - After t = 6.0 , at which the streamer turns up to make the flow complex, the contours are stretched at a higher rate than before. -
This stretching is seen only inside the circle with its radius a little longer
than the major axis of the elliptical vortex,
and the contour lengths in the outside the circle changes much more slowly.
<<index <previous next> |