4.2 Analysis on the Streamfunction
If the perturbation wavenumber is odd ( here, m = 3 ), a streamer is formed on only one of the two vortex edges when the unstable vortex patch is deformed. To make the difference between two edges clear, the flow field in the co-rotating frame with the vortex patch is analyzed. Because the vorticity distribution Q( x,y,t ) is piecewise constant as (2.2), the streamfuction y( x,y,t ) of (2.6) becomes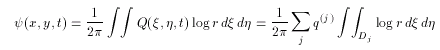 (4.3)
(4.3)
Same as the velocity, the streamfunction can be calculated by line integrations
along the contour:
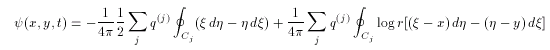 (4.4)
(4.4)
In a rotating frame with a constant angular velocity g,
the velocity is given by
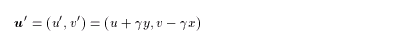 (4.5)
(4.5)
Therefore the streamfunction in the rotating frame can be described as
 (4.6)
(4.6)
By setting γ to be the angular velocity of the unturbed elliptical vortex, we can analyze the growing streamer from the first deformation step of the vortex patch.
Figure 2: Velocity field in the co-rotating frame with the ellipse
(click for the expanded figure).
Thick line is the contour, and arrows are the velocity in the co-rotating frame.
Streamfunctions are displayed in thin lines with color tones.
Blue dots are the stagnation points, and
blue lines are the streamline containing these points.
( t = 0.0 )
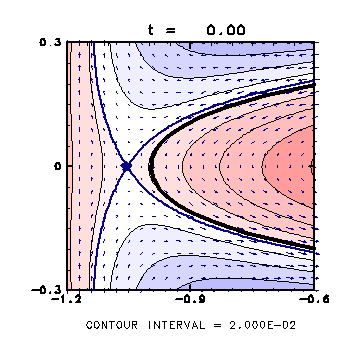

-
In the initial state, the field is almost symmetric with the minor axis.
- The stagnation points are outside of the vortex patch.
- The streamline containing the stagnation points does not cross the contour.
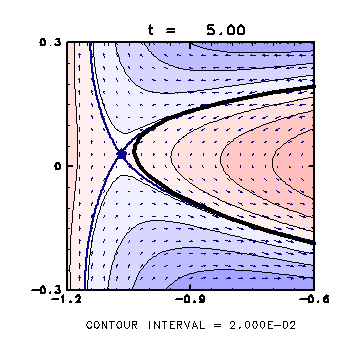
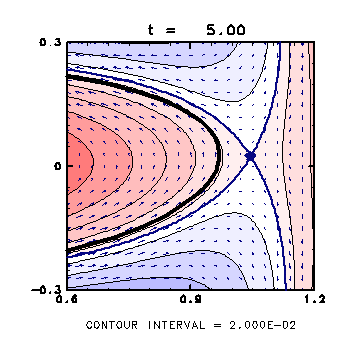
( t = 5.0 )
-
The stagnation point in the left approaches the vortex,
with the streamline containing it coming inside the vortex.
- After this time, the stagnation point comes into the vortex, which causes the streamer formation.
- On the other hand, the stagnation point in the right slowly goes away from the vortex patch.
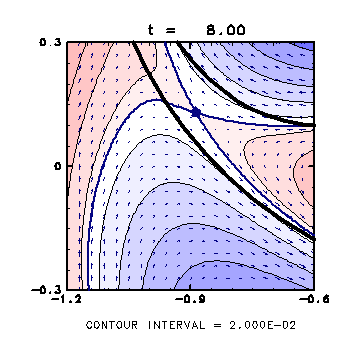
( t = 8.0 )

-
On the left side of the vortex, the stagnation point is inside the streamer.
- The flow crossing the contour exists near the streamer, which deforms the streamer more and more.
- On the right side, on the other hand, the vortex are not deformed very much since the flow is almost parallel to the contour.
Generally, when a fluid particle near the streamline containing a stagnation point comes toward the stagnation point, the particle is to be stretched to the both side of the point. Polvani and Plumb(1992) also argued that the position of stagnation points is very important in the formation of streamer at the edge of a vortex patch.