2.3 Theory of an Elliptical Vortex
In two-dimentional nondivergent perfect fluid, an ellipse is assumed as
(2.12)where λ is the ratio of the major axis to the minor axis, and the initial vorticity is given to be a constant q inside the ellipse and 0 outside.
Such a vortex rotates with a constant angular velocity g,
depending on l and q ( Lamb,1932 ):
(2.13)
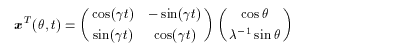(2.14)
Love(1893) examined
the stability of the vortex when the following small perturbation is added:
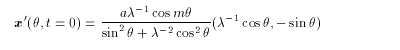(2.15)
- When m = 1 , the perturbation is always neutral.
- When m = 2 , the perturbation is always neutral and does not change in time.
- When m = 3 , the perturbation grows in time and the vortex is unstable if l > 3 .