2.2 Equations of Cotour Dynamics
Basics of contour dynamics are summarized following Dritschel(1989).
The streamfunction Y( x,y,t ) is related to the vorticity Q( x,y,t )
through Poisson's equation,
(2.3)
General solution can be obtained using the Green function G(r):
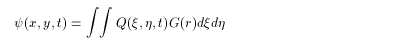(2.4)
where
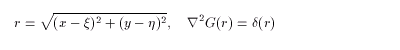(2.5)
As for the two-dimensional infinite plane, G(r) = ( log r )/ 2p :
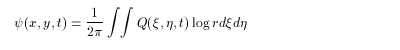(2.6)
The velocity (u,v) is given by
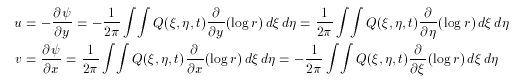(2.7)
By integrating (2.7) partially by h,
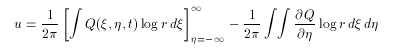(2.8)
The h integral of the second part of the right-hand side is equal to
the vorticity jump q( j ) , since ¶Q/¶h≠0
only on the contour.
Letting q( j ) be the vorticity jump crossing inward,
and taking the line integral anti-clockwise, we obtain
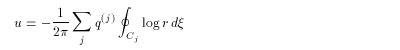(2.9)
Calculating v in the same way yields
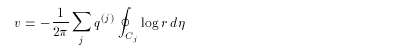(2.10)
These two equations are bound up to
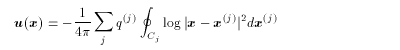(2.11)
which means that the velocity at an arbitrary point can be calculated
from the contour position { x( j ) } .
Since the velocity on the contour can be calculated.
Time evolution of the contour can be computed by advecting the contour using
that velocity.