2.4 Finite-Time Lyapunov Analysis on Fluid Deformation
Yoden and Nomura(1993) did a finite-time Lyapunov analysis in phase space. The same analysis is done here in physical space to introduce a linear measure of deformation of a fluid percel.
Trajectory of a fluid particle is given as a solution of the equation
 (2.16)
(2.16)
Time evolution of a small perturbation from the solution
can be described by a tangent linear equation of (2.16):
 (2.17)
(2.17)
where J is Jacobian matrix of u at x( t ).
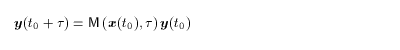 (2.18)
(2.18) (2.19)
(2.19)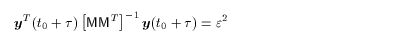 (2.20)
(2.20)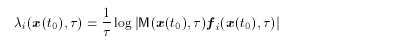 (2.21)
(2.21)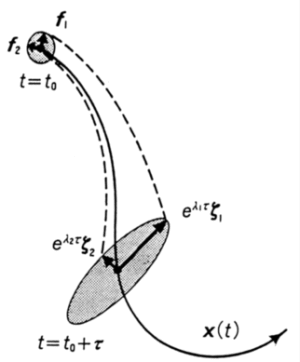 Figure 1: Finite-time lyapunov analysis on fluid deformation.
Figure 1: Finite-time lyapunov analysis on fluid deformation.