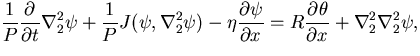 |
(1) |
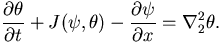 |
(2) |
The governing equations are non-dimensionalized using the thickness of
layer d as length scale, thermal diffusion time 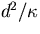 as time scale,
as time scale, 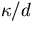 as velocity scale, and
as velocity scale, and 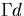 as temperature scale.
as temperature scale. 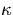 is the thermal diffusivity and
is the thermal diffusivity and 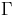 is the absolute value of temperature gradient
of the basic state determined by the heat flux at the boundaries.
is the absolute value of temperature gradient
of the basic state determined by the heat flux at the boundaries. 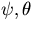 are stream function and temperature
disturbance, respectively.
are stream function and temperature
disturbance, respectively. ![${\displaystyle \Dlapla_2 \equiv \DP[2]{}{x}+\DP[2]{}{z}}$](img15a.gif) is the two-dimensional
Laplacian operator, and
is the two-dimensional
Laplacian operator, and 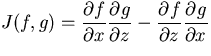 is the Jacobian.
Non-dimensional numbers appearing in the system are the Rayleigh number
is the Jacobian.
Non-dimensional numbers appearing in the system are the Rayleigh number 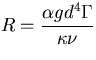 , the Prandtl number
, the Prandtl number 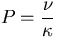 ,
and the parameter of topographic b effect
,
and the parameter of topographic b effect 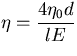 , where
, where 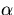 is the thermal expansion coefficient, g
is the gravitational acceleration,
is the thermal expansion coefficient, g
is the gravitational acceleration, 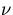 is the kinematic viscosity,
is the kinematic viscosity, 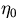 is inclination of the boundaries, l is the size in
the direction of the rotation axis, and E is the Ekman number
is inclination of the boundaries, l is the size in
the direction of the rotation axis, and E is the Ekman number 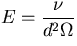 .
.
as time scale,
as velocity scale, and
as temperature scale.
is the thermal diffusivity and
is the absolute value of temperature gradient of the basic state determined by the heat flux at the boundaries.
are stream function and temperature disturbance, respectively.
is the two-dimensional Laplacian operator, and
is the Jacobian. Non-dimensional numbers appearing in the system are the Rayleigh number
, the Prandtl number
, and the parameter of topographic b effect
, where
is the thermal expansion coefficient, g is the gravitational acceleration,
is the kinematic viscosity,
is inclination of the boundaries, l is the size in the direction of the rotation axis, and E is the Ekman number
.