Appendix D: Comparison between the linear theory and the numerical calculations

Table 1: Comparison of growth rates and frequencies between the numerical calculations(Fig.6) and the linear theory. The numerically calculated growth rates and frequencies are obtained by examining the Fourier expansion of y in the x direction at z=0.5.

		k=2p		k=p/4
		Growth rate	Frequency	Growth rate	Frequency
Numerical results		14.5	59.8	0.478	6.20
Linear theory
	Truncation 1	5.54	57.4	0.483	6.83
	Truncation 5	14.6	60.7	0.292	6.93
	Truncation 10	14.6	60.7	0.292	6.93

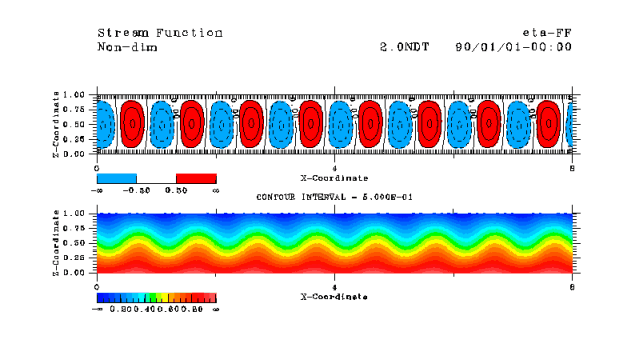
Growth rate and frequency of convection cells with small horizontal scales (k=2p) appearing at the initial stage of the numerical calculations are 15 and 60, respectively. On the other hand, growth rate and frequency from the dispersion relation (9) are 5.5 and 57. The values of frequencies are consistent, while the values of growth rates are not. The reason for this inconsistency is that the truncation of the vertical wave number is too low. From calculation of (7) with higher vertical wave number truncation, growth rate increases to about 15, which is consistent with the results of numerical calculations. Therefore, convection at the initial stage grows according to the linear theory.

(a)Initial stage ** MOVIE **

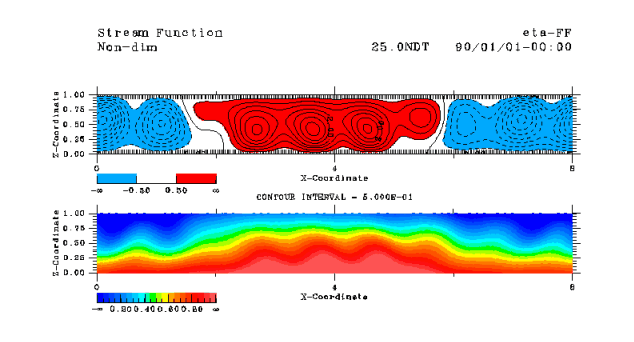
Growth rate and frequency of convection cells with large horizontal scales (k=p/4) appearing at the later stage are 0.48 and 6.2, respectively. On the other hand, growth rate and frequency are 0.48 and 6.8 from the dispersion relation (9). These values seem consistent. However, from the calculation of (7) with higher vertical wave number truncation, the growth rate is 0.29 and frequency is 6.9, revealing inconsistencies in the values of growth rates. Therefore, growth of convection with large horizontal size emerging at the later stage cannot be explained solely by the linear theory. Nonlinear effects should be considered.

(b)Later transition ** MOVIE **

---

Appendix D: Comparison between linear theory and numerical calculations