| In order to confirm the convection behavior obtained by
analyses of the truncated linear system presented so far, we have performed numerical time
integrations of the full system (1)-(4). The computational
domain extends to 8 horizontally and to 1 vertically. The numbers of grid points are 256
horizontally and 32 vertically. The cyclic condition is adopted in the x direction.
4th order Runge-Kutta scheme is used for the time integration and non-linear terms are
discretized by Arakawa's Jacobian scheme (Arakawa 1966). As the
initial condition, a temperature disturbance with an amplitude of 0.01 is placed at x=4
and z=1/4 onto the thermal conductive solution. The Prandtl number and h are fixed at P=1 and h =1000. The numerical computations are performed for the
cases (a) R=10000 and (b) R=8000. In the
large Rayleigh number case (a), there are unstable modes with large and small horizontal
wave numbers, while in the small Rayleigh number case (b), there are only unstable modes
with small horizontal wave numbers. |
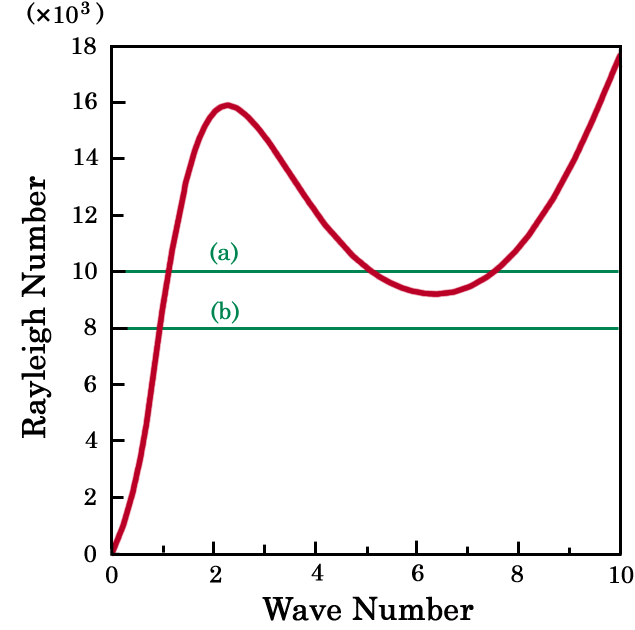 Fig.5 The values of the Rayleigh
number used for the numerical calculations. |
