Measurement of Friction Coefficient on a Powder Layer and Fluid Dynamic Study

As described in Major results 6,  the disk runs in a slanted attitude keeping its head slightly (1-2 mm) above the sliding phase B. From this result, the disk can receives an upward force (called the Newtonian lifting force hereafter) from collision with particles of fluidized powder. 

Consider a moving frame fixed on the disk sliding at velocity V. Assuming that the powder particles undergo perfect elastic collision with the disk, the lifting force for the disk is given by F = 2 r S V2 sin2q cos q, where r is density of  powder, S the basal area of  the disk, and q slope of the disk (Fig 23). To support the disk with basal pressure p, V must be larger than v = ( p / 2 r  sin2q cos q　)1/2.

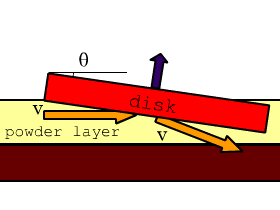Fig. 23.  Schema of  Newtonian lifting force model. The dark blue arrow shows a force provided to the disk by perfect elastic collision between particles and the disk.

Using experimental value of slope (0.6 deg), basal pressure of the disk (745 Pa) and density of powder (0.5×10³ kg/m³), the above equation gives a velocity of 87 m/s. This value is far beyond the critical speed of floatation obtained in the experiments (2-3 m/s). Therefore, this Newtonian lifting force can not be a major source of lifting force for the disk .

Measurement of Friction Coefficient on a Powder Layer and Fluid Dynamic Study