支配方程式はブジネスク流体の方程式系であり,
熱の式, 運動方程式, 連続の式からなる(木村,1983).
ただし, T は温度,
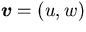 は速度,
は速度,
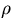 は密度, Pは圧力,
は密度, Pは圧力,
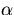 は体膨張率,
は体膨張率,
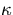 は熱拡散率,
は熱拡散率,
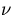 は動粘性率,
は動粘性率,
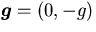 は重力加速度である.
は重力加速度である.
流線関数
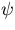 を
を
|
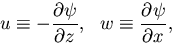 |
(17) |
と導入し,
式 (14),
(15) を書き換えると,
| | |
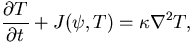 |
(18) |
| | |
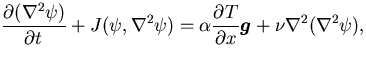 |
(19) |
ただし J(A,B) はヤコビアンであり,
|
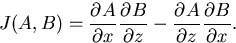 |
(20) |
である.
さらに, 長さを流体層の厚さ b で,
時間を熱拡散時間
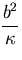 で,
温度を上下面の温度差
で,
温度を上下面の温度差
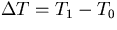 で無次元化する.
すなわち,
で無次元化する.
すなわち,
ここで
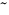 は無次元をあらわしている.
方程式 (18),
(19) は
は無次元をあらわしている.
方程式 (18),
(19) は
| | |
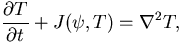 |
(21) |
| | |
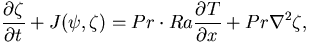 |
(22) |
と書き換えられる.
ここで
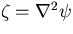 は渦度,
は渦度,
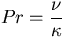 はプランドル数,
はプランドル数,
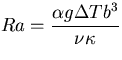 は
レイリー数である. 無次元をあらわす
は
レイリー数である. 無次元をあらわす
 は省略した.
は省略した.
熱的境界条件は, 流体層の上面(z=1),下面(z=0)で
温度固定条件を与える.
|
 |
訂(23) |
運動学的,力学的境界条件は,
境界を突き抜けない条件と Free-slip 条件を与える.
|
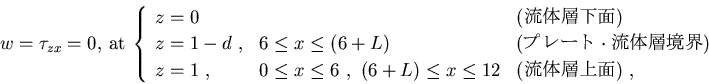 |
(24) |
|
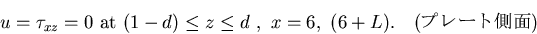 |
(25) |
水平方向には周期的条件を与える.
これらの条件を渦度と流線関数の条件として与えなければならない.
流体が境界を突き抜けない条件は,
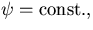 |
| |
(26) |
となる. さらに, 初期条件として静止状態
(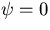 )を与えるので,
流線関数は境界において
)を与えるので,
流線関数は境界において
|
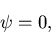 |
(27) |
でなくてはならない. また, Free-slip条件は,
水平な境界面において w=0 を考慮して
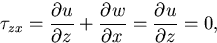
すなわち
|
![\DP[2]{\psi}{z}=0,](../../takehiro/japanese/img70.gif) |
(28) |
となる. また(27)より
水平な境界面においては
![\DP[2]{\psi}{x}=0,](../../takehiro/japanese/img71.gif)
であるから, 渦度
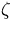 が境界において,
が境界において,
|
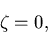 |
(29) |
となる.
鉛直な境界面においても同様に行うことにより
(29) が得られる.
は速度,
は密度, Pは圧力,
は体膨張率,
は熱拡散率,
は動粘性率,
は重力加速度である.
を
で, 温度を上下面の温度差
で無次元化する. すなわち,
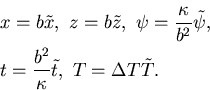
は無次元をあらわしている. 方程式 (18), (19) は
は渦度,
はプランドル数,
は レイリー数である. 無次元をあらわす
は省略した.
)を与えるので, 流線関数は境界において
が境界において,