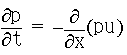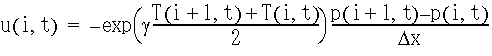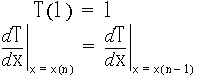付録5-1. 数値実験の基礎方程式と一次元モデル
(EQ 4)が時間発展形でないため，このままでは時間発展的に数値実験を行うことは困難である．そこで，仮の圧縮率
を導入して状態方程式と連続の式
 |
(EQ 12) |
 |
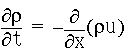(EQ 13) |
を考えると，これらより
を得る．
数値実験では(EQ 3)，(EQ 4)，(EQ 14)の３つの方程式で記述される系の時間発展を調べるが，初期状態から定常状態に至るまでの間の
の変化量が十分小さく(2%未満)，近似的に非圧縮とみなせるような
を初期値として与える．
| 図 21. 数値実験のグリッド配置 |
|---|
|
： ， ， の定義点
： の定義点
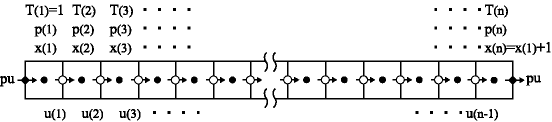
：流入点と流出点での流量 を境界条件として与える座標  は となるようにとる． |
図21のようにグリッドを配置し(EQ 3)，(EQ 4)，(EQ 14)をそれぞれ
のように差分化し，４次のルンゲ・クッタ法を用いる．初期の
，
，
を
|
(EQ 18) |
|
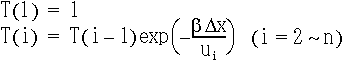
(EQ 19) |
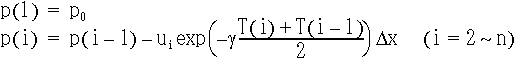 ただし，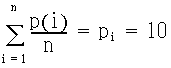 
|
(EQ 20) |
とし，温度
の境界条件を
圧力
と流速
の境界条件を入口と出口で
|
(EQ 22) |
とし流量を与える．
，
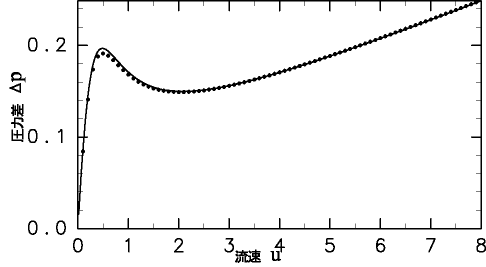
のときの(EQ 5)のグラフと，
方向に
の格子をとり，流速の境界条件を
の範囲で0.1刻みに変えて行った数値実験で得た定常状態の
のプロットとを比較したものが図22である．
と理論値との比較（
，
）
印が数値実験による値，実線は