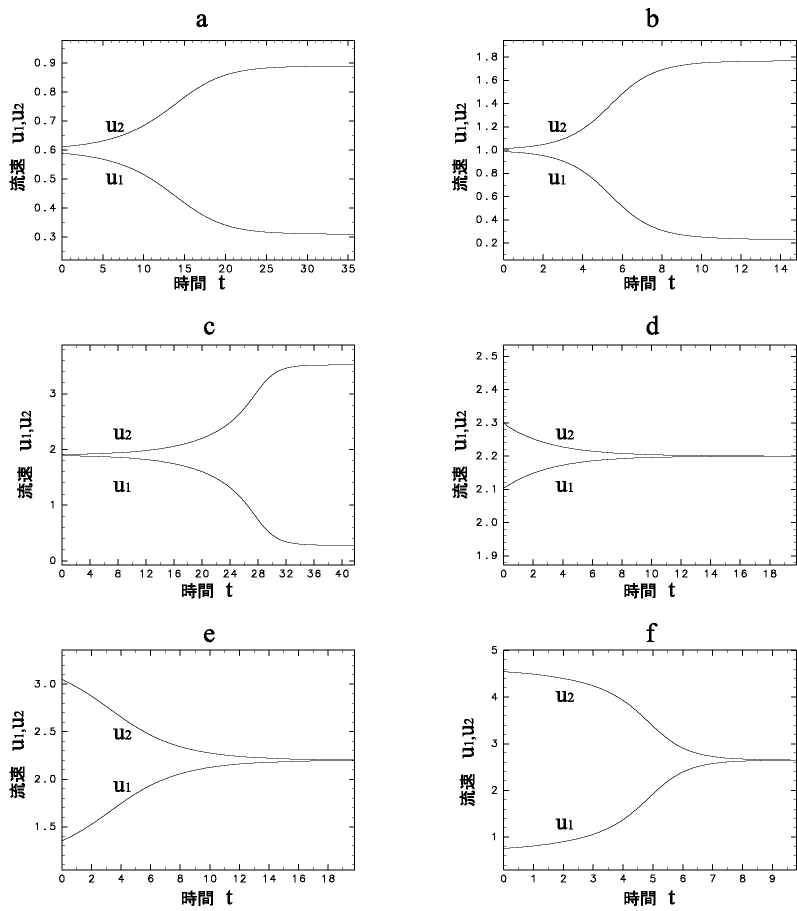
２本並列モデルの数値実験a，b，c，d，e，fの流速の変化を，縦軸に流速
，横軸に時間
をとってグラフにしたものを図24に示す．AB近傍の初期状態からAB2上の定常状態へ，BC2近傍の初期状態からBC上の定常状態へと状態が変化することから，AB，BC2上の状態が不安定，AB2，BC上の状態が安定であることがわかる．また，流れの対称性よりAC1上の状態は安定，BC1上の状態は不安定である．
| 図 24. ２本並列モデルの数値実験の流速変化 |
|---|
 |
a:初期の流速を図7のAB近傍の状態( 
,
)=(0.59,0.61)で与えると，AB2上の状態(0.31,0.89)で定常になる．( =0.60)b:同様にAB近傍の初期状態(0.99,1.01)からAB2上の定常状態(0.23,1.77)へ．(  =1.00)c:AB近傍の初期状態(1.89,1.91)からAB2上の定常状態(0.28,3.52)へ．(  =1.90)d:BC近傍の初期状態(2.10,2.30)からBC上の定常状態(2.20,2.20)へ．(  =2.20)e:BC2近傍の初期状態(1.35,3.05)からBC上の定常状態(2.20,2.20)へ．(  =2.20)f:BC2近傍の初期状態(0.75,4.55)からBC上の定常状態(2.65,2.65)へ．(  =2.65) |
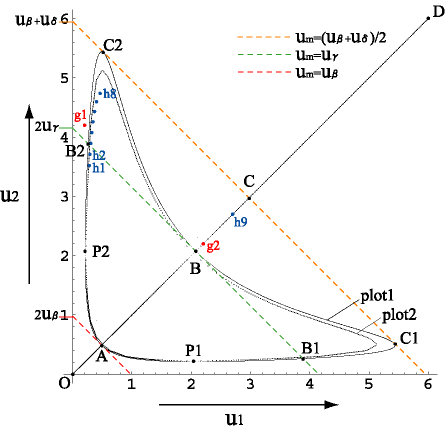
初期状態としてB2C2の近傍の流速を与えてB2C2上の平衡状態を作ることは難しく，たとえば図25でg1(0.20, 4.20)を初期状態として与えるとBC上の状態g2(2.20,2.20)に移ってしまうが，実験c（
）で得られた平衡状態（図25のh1）の
と
を初期値として与えて，流速
の境界条件を0.1増加させ，平衡状態になったのちにさらに0.1増加する，という方法で少しずつ流量を増やしていくことでB2C2上の流れに相当する平衡状態が得られ（図25のh2からh8に至る青点），
で一様な平衡状態になる（h9）．このことから，B2C2，B1C1上の点で表される平衡状態は安定であるものの，その安定性はBC上の点で表される状態に比べて弱く，またC2に近づくほど弱くなっているものと思われる．
図25では，plot2として，一次元モデルの数値実験で得られた
特性（図22）から得られる
の解をプロットしてある（plot1は理論値をもとに得られる解）．２本並列モデルの数値実験では，管の入口と出口にある
方向の流れ（図23の
と
）の影響で，h1からh8の定常状態はplot2から少しずれている．
| 図 25. B2C2の解の安定性 |
|---|
 |