5-1. 流れの状態の分類
ここまでで，流体の粘性の温度依存を考慮すると一次元流れで負性抵抗が現れること，さらに一次元流れを並列に２本，３本と束ねたモデルで負性抵抗が現れるような境界条件を課したときに定常解の分岐により非一様な定常流が現れることをみた．次に，さらに管の数を増やしていったときに一般にどのような流れの状態が定常解として存在し，そのうち安定な流れとして存在できるものはどれであるのか，ということを考える．
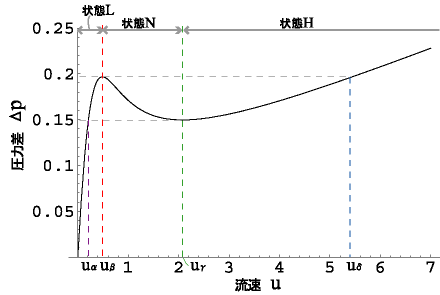
今，１本の管の流れの状態に注目し，その流速が
のときに状態L(Low)，
のときに状態N(Negative)，
のとき状態H(High)と呼ぶことにする(図10)と，たとえば２本並列モデルで一方の流れがL，他方がHであればLH，両方がHであればHH，というように，一次元流れを複数束ねたモデルについても流れの状態をL，N，Hの組み合わせで表現することができる．このとき，流れの対称性からLHとHLは同じ状態とみなし，LHという表記で統一する．すなわち，流速の遅い状態から先に，L，N，Hの順で書く．
