|
3.d. Intensity of Convection (2): Conduction Layer
|
The vertical gradient of potential temperature below approximately 50
m is in good agreement with that described by turbulent diffusion.
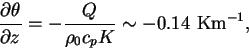 |
(2) |
where 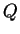 is heat flux.
In evaluating Equation (2) , we have adopted is heat flux.
In evaluating Equation (2) , we have adopted  ≈ 30
W m-2 which was obtained from the total amount of infrared
radiative heating and sensible heat flux at around 12:00 LT. ≈ 30
W m-2 which was obtained from the total amount of infrared
radiative heating and sensible heat flux at around 12:00 LT.
 = 2×10-2 kg
m-3, = 2×10-2 kg
m-3, 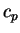 = 734.9 J kg-1 K-1,
and = 734.9 J kg-1 K-1,
and 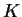 = 15 m2
sec-1 were obtained from the turbulent diffusion
coefficient calculated in our numerical model. The region below ~50
m in the thermal boundary layer can be referred to as the conduction
layer. = 15 m2
sec-1 were obtained from the turbulent diffusion
coefficient calculated in our numerical model. The region below ~50
m in the thermal boundary layer can be referred to as the conduction
layer.
Provided that the temperature structure of the conduction layer is
given by Equation (2),
let us estimate the depth of conduction layer
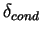 and potential temperature difference and potential temperature difference 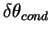 of the layer.
The flux Rayleigh number of the conduction layer is given as of the layer.
The flux Rayleigh number of the conduction layer is given as
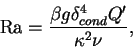 |
(3) |
where 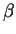 is thermal expansion coefficient, is thermal expansion coefficient, 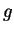 is gravitational acceleration, is gravitational acceleration, 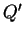 is temperature flux ( is temperature flux (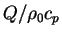 ), and ), and
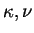 are thermal diffusion coefficient and
kinematic viscosity, respectively. Convective instability is expected
to appear when the flux Rayleigh number exceeds the critical value.
Supposing that are thermal diffusion coefficient and
kinematic viscosity, respectively. Convective instability is expected
to appear when the flux Rayleigh number exceeds the critical value.
Supposing that
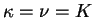 and and 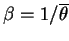 , the
depth of conduction layer can be estimated by using Equation
(2) as , the
depth of conduction layer can be estimated by using Equation
(2) as
 |
(4) |
According to linear stability analysis, the order of magnitude of the
critical Rayleigh number for fixed heat flux boundary condition is 100
(Sasaki, 1970). Substituting this, we
obtain 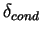 ≈ 57 m, and from Equation
(2), we have ≈ 57 m, and from Equation
(2), we have 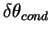 ≈ 8K.
Although the values of conduction layer thickness and potential
temperature difference at 14:00 LT shown
in Figure. 7 ( ≈ 8K.
Although the values of conduction layer thickness and potential
temperature difference at 14:00 LT shown
in Figure. 7 (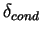 < 50
m, < 50
m, 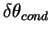 ≈ 6K) are slightly smaller than those
obtained above, they are fairly acceptable as order estimations. ≈ 6K) are slightly smaller than those
obtained above, they are fairly acceptable as order estimations.
|