|
B.a.iii. Diagnostic equation of the pressure function
|
Before deriving the finite difference equation,
Equation (A.8)
is transformed as follows.
(The definition of
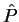 is described in Appendix B.a.i.).
This equation can be solved by using the dimension reduction
method. The finite difference form of the pressure equation can be
written in matrix form.
is described in Appendix B.a.i.).
This equation can be solved by using the dimension reduction
method. The finite difference form of the pressure equation can be
written in matrix form.
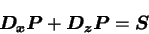 |
(B.19) |
where
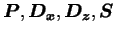 are matrixes whose elements are in finite difference form for the following terms. are matrixes whose elements are in finite difference form for the following terms.
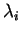 and and 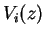 are the eigenvalue and eigenvector of
are the eigenvalue and eigenvector of
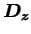 .
By using the eigenvalue matrix .
By using the eigenvalue matrix
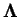 and the eigenvector matrix
and the eigenvector matrix
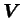 of
of
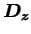 , ,
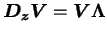 .
Expanding so .
Expanding so
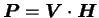 ,
Equation (B.19) can be rewritten as follows. ,
Equation (B.19) can be rewritten as follows.
Therefore,
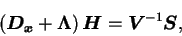 |
(B.20) |
The elements of matrix
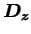 , which are required to derive eigenvalue
, which are required to derive eigenvalue
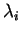 and eigenvector
and eigenvector
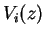 ,
are evaluated in finite form as ,
are evaluated in finite form as
Second- and fourth-order centered schemes are used since space
differencing in the continuity equation is evaluated by a fourth-order
centered scheme while space differencing in the pressure gradient term
is evaluated by a second-order centered scheme.
Therefore,
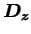 is a quint-diagonal matrix.
is a quint-diagonal matrix.
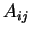 , which is element of , which is element of
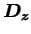 , is represented as follows. , is represented as follows.
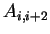 |
 |
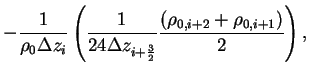 |
(B.21) |
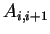 |
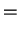 |
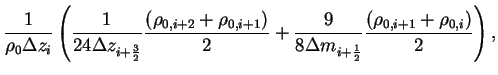 |
(B.22) |
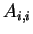 |
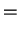 |
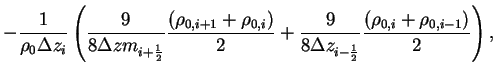 |
(B.23) |
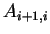 |
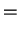 |
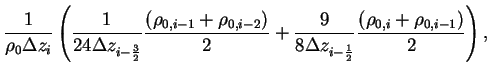 |
(B.24) |
 |
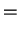 |
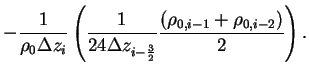 |
(B.25) |
Boundary conditions are 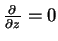 at the lower and upper boundary. at the lower and upper boundary.
The horizontally-dependent terms are expanded by using an
eigenfunction. In this model, we use a Fourier series.
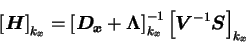 |
(B.29) |
|