|
The model atmosphere is described by a two-dimensional anelastic system
(Ogura and Phllips, 1962). The effect
of planetary rotation is not considered.
(A.1),
(A.2)
are the horizontal and vertical components of the equation of motion, respectively.
(A.3) is the continuity equation and
(A.4) is the thermodynamic equation.
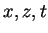 are the horizontal, vertical and time coordinates, respectively.
are the horizontal, vertical and time coordinates, respectively.
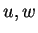 are horizontal and vertical wind velocity, respectively.
are horizontal and vertical wind velocity, respectively.
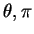 are perturbation of potential temperature and non-dimensional pressure function
from the basic state, respectively
are perturbation of potential temperature and non-dimensional pressure function
from the basic state, respectively
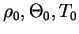 are density, potential temperature and temperature in the basic state.
are density, potential temperature and temperature in the basic state.
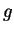 is gravitational acceleration whose value is equal to 3.72 m sec-2
is gravitational acceleration whose value is equal to 3.72 m sec-2
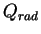 is the radiative heating (cooling) rate per unit mass, which is
described in Appendix A.d in detail.
is the radiative heating (cooling) rate per unit mass, which is
described in Appendix A.d in detail.
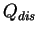 is the heating rate per unit mass owing to the dissipation of
turbulent kinetic energy, which is given by the
turbulent parameterization.
is the heating rate per unit mass owing to the dissipation of
turbulent kinetic energy, which is given by the
turbulent parameterization.
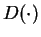 in Equations
(A.1) ∼
(A.4) represents turbulent
diffusion, which is caused by subgrid-scale turbulent mixing as
follows. in Equations
(A.1) ∼
(A.4) represents turbulent
diffusion, which is caused by subgrid-scale turbulent mixing as
follows.
| |
|
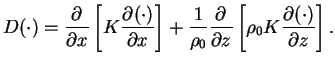 |
(A.5) |
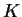 is the turbulent diffusion coefficient and is calculated by Equations
(A.9) and
(A.10).
is the turbulent diffusion coefficient and is calculated by Equations
(A.9) and
(A.10).
The non-dimensional pressure function 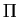 and potential
temperature and potential
temperature 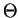 are defined as follows. are defined as follows.
Where 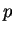 and and 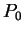 are pressure and pressure in the basic state, are pressure and pressure in the basic state, 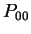 is the reference pressure (
= 7 hPa), is the reference pressure (
= 7 hPa),
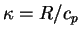 and and 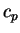 is the specific heat at constant pressure per unit mass, is the specific heat at constant pressure per unit mass,
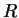 is the atmospheric gas constant per unit mass. is the atmospheric gas constant per unit mass.
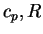 are set as those of CO2 (
734.9 J kg-1 K-1, 189.0 J kg-1 K-1,
respectively).
The basic state of the atmospheric structure is calculated by using
the hydrostatic equation and equation of state for ideal gas, as
follows. are set as those of CO2 (
734.9 J kg-1 K-1, 189.0 J kg-1 K-1,
respectively).
The basic state of the atmospheric structure is calculated by using
the hydrostatic equation and equation of state for ideal gas, as
follows.
The perturbation of the non-dimensional pressure function 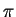 is diagnosed
by using the following equation, which is derived from Equations
(A.1) ∼ (A.3). is diagnosed
by using the following equation, which is derived from Equations
(A.1) ∼ (A.3).
|