|
理想気体を仮定した鉛直 1 次元大気の温位は以下の式を用いて計算する.
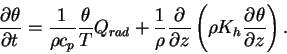 |
(C.1) |
ここで 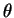 は温位, は温位, 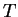 は温度, は温度, 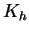 は鉛直拡散係数, は鉛直拡散係数, 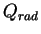 は放射による単位体積あたりの加熱率,
は放射による単位体積あたりの加熱率, 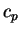 は定圧比熱である. は定圧比熱である. 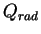 は CO2
の放射伝達方程式を解いて得られる放射フラックスの収束によって与えられる
(付録 A.d.i 節参照).
ダストの放射過程は考慮しない.
右辺第 2 項は対流による熱輸送を拡散でパラメタライズしたものである. は CO2
の放射伝達方程式を解いて得られる放射フラックスの収束によって与えられる
(付録 A.d.i 節参照).
ダストの放射過程は考慮しない.
右辺第 2 項は対流による熱輸送を拡散でパラメタライズしたものである.
さらに大気は静水圧平衡にあるとする.
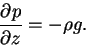 |
(C.2) |
鉛直拡散係数 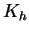 は
Gierasch and Goody (1968)
で用いられた方法で計算する. は
Gierasch and Goody (1968)
で用いられた方法で計算する.
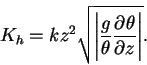 |
(C.3) |
ここで 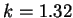 である
(Priestley, 1959). である
(Priestley, 1959).
地表面からの熱フラックス 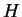 の計算も Gierasch and Goody (1968)
で用いられた方法で行う.
の計算も Gierasch and Goody (1968)
で用いられた方法で行う.
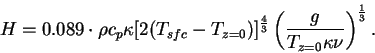 |
(C.4) |
ここで 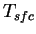 は地表面温度, は地表面温度, 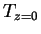 は地表気温, は地表気温, 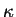 は大気の熱拡散係数, は大気の熱拡散係数, 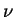 は大気の動粘性係数で, 値は Gierasch and Goody
(1968) に従う(それぞれ 8×10-4 m2sec-1,
1×10-3 m2sec-1).
ただし地表気温が地表面温度よりも高い場合には熱フラックスは 0 とする. は大気の動粘性係数で, 値は Gierasch and Goody
(1968) に従う(それぞれ 8×10-4 m2sec-1,
1×10-3 m2sec-1).
ただし地表気温が地表面温度よりも高い場合には熱フラックスは 0 とする.
地表面温度 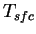 は熱伝導方程式を解いて計算する
(付録 A.e 節参照). は熱伝導方程式を解いて計算する
(付録 A.e 節参照).
|