|
大気は 2 次元の非弾性方程式系
(Ogura and Phllips, 1962)
でモデル化する. 惑星の自転効果は考慮しない.
(A.1),
(A.2)
はそれぞれ水平および鉛直方向の運動方程式,
(A.3) は連続の式,
(A.4) は熱力学の式である. 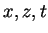 はそれぞれ水平, 鉛直, 時間座標, はそれぞれ水平, 鉛直, 時間座標, 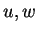 はそれぞれ水平風速と鉛直風速, はそれぞれ水平風速と鉛直風速, 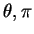 はそれぞれ温位と無次元圧力関数の基本場からの偏差である.
はそれぞれ温位と無次元圧力関数の基本場からの偏差である.
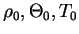 はそれぞれ基本場の密度と温位, 温度である. はそれぞれ基本場の密度と温位, 温度である. 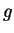 は重力加速度であり, ここでは は重力加速度であり, ここでは 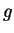 = 3.72 msec-2 とする. = 3.72 msec-2 とする. 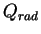 は放射加熱(冷却)であり, 後述の
放射過程 により与えられる.
は放射加熱(冷却)であり, 後述の
放射過程 により与えられる.
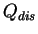 は乱流エネルギーの散逸による加熱であり, 後述の
乱流パラメタリゼーション から与えられる.
(A.1) 〜
(A.4) 式中の は乱流エネルギーの散逸による加熱であり, 後述の
乱流パラメタリゼーション から与えられる.
(A.1) 〜
(A.4) 式中の 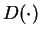 項は数値モデルの空間格子間隔以下の乱流による混合の寄与で, 以下のように表される.
項は数値モデルの空間格子間隔以下の乱流による混合の寄与で, 以下のように表される.
| |
|
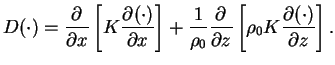 |
(A.5) |
ここで 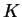 は (A.9),
(A.10)
式で計算される乱流拡散係数である.
は (A.9),
(A.10)
式で計算される乱流拡散係数である.
無次元圧力関数 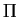 と温位 と温位 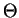 は以下の式で定義される. は以下の式で定義される.
ここで 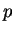 は圧力, は圧力, 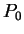 はその基本場の値, はその基本場の値, 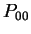 は参照気圧(
= 7 hPa), は参照気圧(
= 7 hPa),
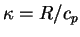 である. である. 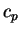 は単位質量あたりの定圧比熱, は単位質量あたりの定圧比熱,
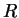 は単位質量あたりの気体定数である. は単位質量あたりの気体定数である. 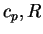 は CO2 の値(それぞれ
734.9 Jkg-1K-1, 189.0 Jkg-1K-1)
を使用する.
基本場の温度圧力構造は静水圧の式と理想気体の状態方程式から計算される. は CO2 の値(それぞれ
734.9 Jkg-1K-1, 189.0 Jkg-1K-1)
を使用する.
基本場の温度圧力構造は静水圧の式と理想気体の状態方程式から計算される.
無次元圧力関数の偏差 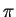 は (A.1)
〜 (A.3)
式を変形して得られる以下の式から診断される. は (A.1)
〜 (A.3)
式を変形して得られる以下の式から診断される.
|