|
波数 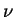 の光に対する光学的厚さ の光に対する光学的厚さ 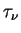 は, 単位体積あたりの消散係数 は, 単位体積あたりの消散係数
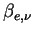 を用いて を用いて
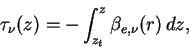 |
(A.39) |
と表される. ここで 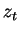 は大気上端高度である. は大気上端高度である.
 は は
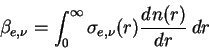 |
(A.40) |
と表される. ここで
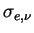 は消散断面積
(extinction cross section), は消散断面積
(extinction cross section), 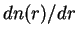 は散乱物質の粒径分布関数である
(cf. Liou, 1980; 柴田, 1999). 質量消散係数 は散乱物質の粒径分布関数である
(cf. Liou, 1980; 柴田, 1999). 質量消散係数  との関係は, との関係は,
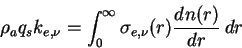 |
(A.41) |
となる. ここで 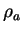 は大気の密度, は大気の密度, 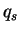 は散乱物質の質量混合比である.
同様に単位体積あたりの散乱係数, 吸収係数は, 散乱断面積
(scattering cross section) は散乱物質の質量混合比である.
同様に単位体積あたりの散乱係数, 吸収係数は, 散乱断面積
(scattering cross section)
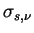 , 吸収断面積(absorption
cross section) , 吸収断面積(absorption
cross section)
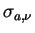 を用いて を用いて
と表される. この場合一次散乱アルベド
 は は
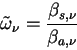 |
(A.44) |
となる.
消散断面積を幾何学的断面積で割った値を消散効率
(extinction efficiency )と呼び, これを 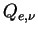 と表す. と表す.
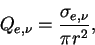 |
(A.45) |
同様に散乱効率 (scattering efficiency) 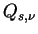 , 吸収効率
(absorption efficiency) , 吸収効率
(absorption efficiency) 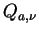 が定義される. が定義される.
本研究における計算では, ダストの質量混合比 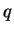 を既知の物理量としてダストの光学的厚さを求める.
与えられるパラメータは粒径分布で平均された消散効率と を既知の物理量としてダストの光学的厚さを求める.
与えられるパラメータは粒径分布で平均された消散効率と
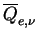 , 一次散乱アルベド , 一次散乱アルベド
 , 粒径分布関数 , 粒径分布関数 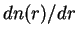 , そのモード半径 , そのモード半径 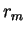 と有効半径
(断面積加重平均半径 (cross section weighted mean radius) ともいう) と有効半径
(断面積加重平均半径 (cross section weighted mean radius) ともいう) 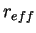 , そしてダストの密度 , そしてダストの密度 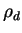 である. である.
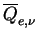 , , 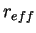 はそれぞれ はそれぞれ
で与えられる.
散乱物質の形状を球形と仮定すると単位質量あたりの消散係数は,
となる. ここで 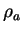 は大気の密度である. したがって光学的厚さは は大気の密度である. したがって光学的厚さは
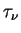 は は
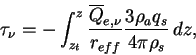 |
(A.51) |
となる.
|