付録: 運動エネルギーの式 目次
線形化した回転円筒モデルの渦度方程式は,


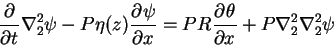
\begin{displaymath} \DP{}{t}\Dlapla_2\psi - P\eta(z)\DP{\psi}{x} = PR\DP{\theta}{x} + P\Dlapla_2\Dlapla_2 \psi \end{displaymath} (C.1)

である. ψ をかけて変形していくと, 各項はそれぞれ

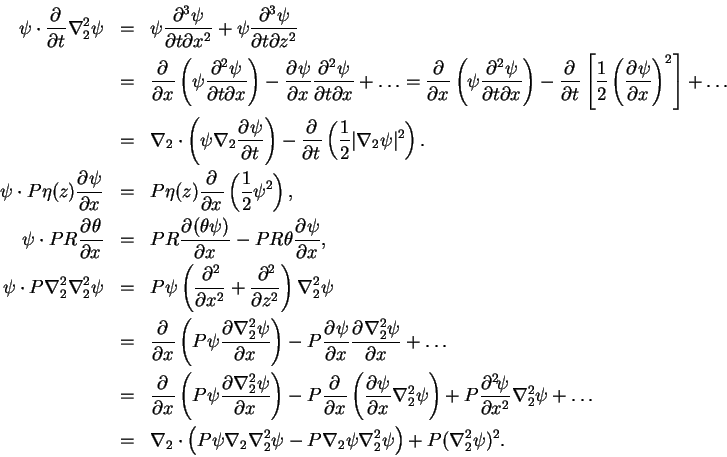
   \begin{eqnarray*} \psi\cdot \DP{}{t}\Dlapla_2\psi &=& \psi \frac{\partial^3 \... ...\psi -P\Dgrad_2\psi\Dlapla_2\psi\right) +P(\Dlapla_2\psi)^2. \end{eqnarray*}

ただし ▽2 は 2 次元のナブラ演算子である. したがって, 運動エネルギーの式は

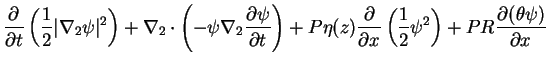
$\displaystyle \DP{}{t}\left(\frac{1}{2}\vert\Dgrad_2\psi\vert^2\right) + \nabla......ight)+ P\eta(z)\DP{}{x}\left(\frac{1}{2}\psi^2\right) + PR\DP{(\theta\psi)}{x}$
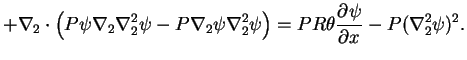
$\displaystyle + \nabla_2\cdot\left(P\psi\Dgrad_2\Dlapla_2\psi -P\Dgrad_2\psi\Dlapla_2\psi\right) = PR\theta\DP{\psi}{x}-P(\Dlapla_2\psi)^2.$ (C.2)

さらに x 方向に平均をとれば,

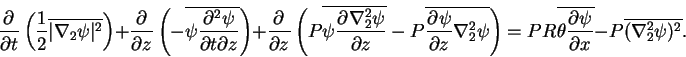
\begin{displaymath} \DP{}{t}\left(\frac{1}{2}\overline{\vert\Dgrad_2\psi\vert^2... ...overline{\theta\DP{\psi}{x}} -P\overline{(\Dlapla_2\psi)^2}. \end{displaymath} (C.3)

ここで上線は x 方向への 1 波長平均を表している. 左辺第 1 項が運動エネルギーの時間変化, 第 3 項は粘性による運動エネルギー輸送の収束である. 右辺第 1 項は浮力による運動エネルギーの生成, 第 2 項が粘性による運動エネルギーの散逸に対応している.

左辺第 2 項はロスビー波の伝播に伴う運動エネルギーの収束であると解釈できる. 波型の解を仮定するとこの項の表すエネルギー流束がロスビー波の群速度に運動エネルギーをかけたものとなっていることが示される( Pedlosky 1987).

付録: 運動エネルギーの式 目次