付録:非線形計算詳細

有限振幅での対流の様子を調べるための数値計算の方法と設定は パラメターηの与え方を除けば 竹広ら (1998) とほぼ同じである.

• 計算領域は水平方向に 4 ,鉛直方向に1 であり, 水平方向に 128 点, 鉛直方向に 32 点のグリッドポイントを配置.
• 水平方向の境界条件は周期的.
• 水平, 鉛直方向ともに有限差分を適用. 非線形項は Arakawa のヤコビアンスキームを用いた.
• 時間積分には 4 次の Runge-Kutta スキームを用いた.
• 初期値は, 熱伝導解に対して x=2, z =1/4 に振幅 0.01 の温度擾乱をおいたもの.
• レイリー数はいずれの場合も臨界値の約 1.3 倍程度.

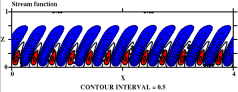
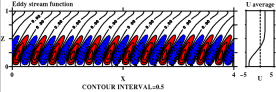
E=10-4	温度場	流線関数	平均流と擾乱の流線関数
P=0.1, R=1.3x105
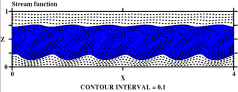
P=1, R=4x105
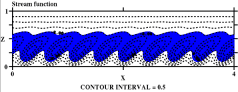
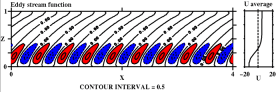
P=10, R=8x105

付録:非線形計算詳細