4. SPMODEL Programming

SPMODEL: A Series of Hierarchical Spectral Models for GFD << Prev | Index| Next >>

4. SPMODEL Programming

4.1. Programing procedure in SPMODEL

In this section, we explain a typical programming procedure for fluid calculations with the spectral method using the SPMODEL library. For the fundamentals on numerical fluid calculations with the spectral method, please refer to other more appropriate textbooks such as [5]. The following is the procedure:

Select a module of SPMODEL library which is appropriate for the geometry of the computational domain and boundary conditions.
Derive spectral-transformed governing equations in a formal manner.
Apply an appropriate finite difference scheme for time derivatives in the governing equations.
Simply express the code according to the formulation developed at the stages 2 and 3.

As an example, let us construct a program for computing the time development of the Korteweg-deVries equation in a one-dimensional domain whose length is L under the cyclic boundary condition. The governing equation is

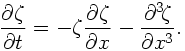
1. The module utilized is the one for one-dimensional domain with cyclic boundaries which is shown as an example in Section 3.

2. The Fourier transform and its inversion with respect to the spatial dimension x are defined as

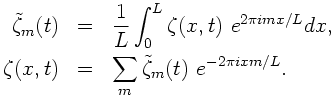
The governing equation is then transformed as

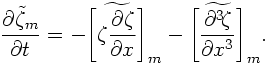
Here, the tilde and the subscript denote the wavenumber component of the Fourier transform.

3. If, for example, the Euler scheme is applied for the time derivative, we have,

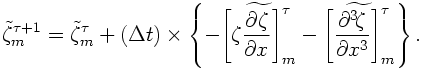
Superscripts τ and τ+1 denote the present and next time steps, respectively.

4. From the above formulation, we can write down the loop part of the program for time integration as follows:

do it=1,nt
    e_Zeta = e_Zeta + dt * &
            ( -e_g(g_e(e_Zeta)*g_e(e_Dx_e(e_zeta))) & 
              - e_Dx_e(e_Dx_e(e_Dx_e(e_zeta)))  ) 
enddo

For the evaluation of the nonlinear term, the above program employs the transformed method, in which the spectral data are transformed back to real space, the product term evaluated on the grid points of the real space, and then transformed forward to the spectral space again.

4.2. The advantages of SPMODEL programming

Facility of programming

Note that, in the above example, the main part of the final source program code shows a good correspondence with the original mathematical expression of the governing equation. This is the most advantageous point of SPMODEL programming. Although the spectral numerical method is utilized, the corresponding program code can be written down directly when the governing equations are simple. The reference manual is rarely needed during programming, since the action of the functions and the spaces where the input and output data are defined can be easily recognized from their names owing to the systematic naming convention.

In contrast, the conventional (FORTRAN77) programming of the spectral numerical method required tremendous efforts for deriving the explicit expression of each spectral component equation which includes wavenumbers and interaction terms with other spectral elements.
Readability of program source codes

Since program source codes are written in a similar form to the original mathematical expressions, the programs can be understood easily.

In contrast, in the conventional (FORTRAN77) programming of the spectral numerical method, it was quite difficult to recognize the original governing equations from the program source codes, since the expressions formulated for programming were greatly modified from the original mathematical expressions of the governing equations.
Facility of modification or alteration

Thanks to the above two features, we can modify or alter the programs quite easily.