5.1. 1 次元周期境界領域での KdV 方程式

階層的地球流体スペクトルモデル集 SPMODEL << Prev | Index| Next >>

5.1. 1 次元周期境界領域での KdV 方程式

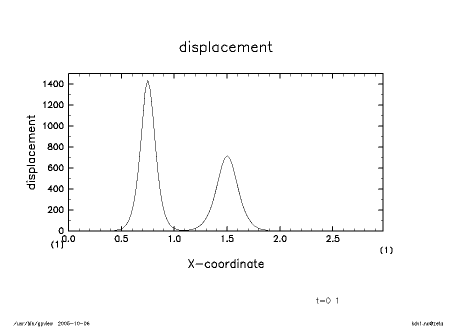
振幅の異なる 2 つのソリトン解のすり抜けの計算例である. 支配方程式と用いているモジュールは既に第 4 節にて示してあるが, 以下に再掲する. KdV 方程式およびその解析解については参考文献 [6], [7] を参照されたい.

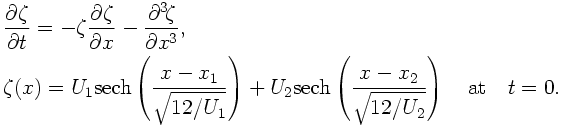
第 1 式が支配方程式の KdV 方程式, 第 2 式が初期条件であり, U₁, x₁, U₂, x₂ がそれぞれ 2 つのソリトン解の振幅と中心座標を表している.

これらをプログラミングしたソースコードの全体が kdv1.f90である. 初期条件は

g_Zeta= U1*sech((g_X-X1)/sqrt(12/u1))**2 &
        + U2*sech((g_X-X2)/sqrt(12/u2))**2

支配方程式は Leap frog スキームで時間積分を行なっており

do it=1,nt
    e_Zeta = e_Zeta0 + 2*dt * & 
            ( -e_g(g_e(e_Zeta1)*g_e(e_Dx_e(e_Zeta1))) &
              - e_Dx_e(e_Dx_e(e_Dx_e(e_Zeta1)))  )
    e_Zeta0=e_Zeta1 ; e_Zeta1=e_Zeta
    ...
enddo

となっている. 初期条件も Fortran90 の配列機能により 1 行で書けていることに注目されたい.

[animation]