The basic equations utilized are same as TI2006: the horizontal structure equations of a primitive system using an equatorial β-plane approximation. Dissipation is excluded. We consider a channel extending along longitudinal direction infinitely. At both the north and south boundaries, meridional velocities are set to zero. The x- and y-axes are along the longitudinal and meridional directions, respectively. The equator is located at y=0. By expanding variables in zonal harmonics in the same manner as Dunkerton (1993), non-dimensional perturbation equations linearized about a linear shear flow are
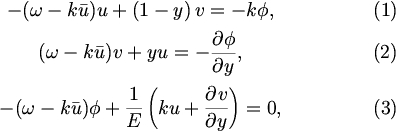
where
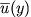 ,
,
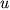 ,
,
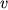 ,
and
,
and
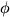 are the basic zonal velocity, perturbation zonal velocity, meridional
velocity, and geopotential, respectively.
Meridonal velocity
are the basic zonal velocity, perturbation zonal velocity, meridional
velocity, and geopotential, respectively.
Meridonal velocity
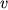 is defined to be out of phase with
is defined to be out of phase with
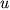 and
and
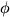 .
.
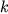 and
and
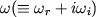 are zonal wavenumber and complex frequency, respectively.
The above equations are non-dimensionalized by
the length scale
are zonal wavenumber and complex frequency, respectively.
The above equations are non-dimensionalized by
the length scale
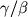 which is the latitudinal width of
the inertially unstable region,
time scale
which is the latitudinal width of
the inertially unstable region,
time scale
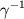 ,
velocity scale
,
velocity scale
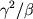 ,
and geopotential scale
,
and geopotential scale
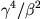 ;
;
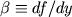 (
(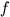 is the Coriolis parameter)
and
is the Coriolis parameter)
and
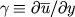 .
The only non-dimensional parameter is
.
The only non-dimensional parameter is
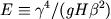 ,
where
,
where
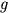 and
and
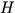 are gravitational constant and equivalent depth, respectively.
are gravitational constant and equivalent depth, respectively.
In this paper, same as TI2006, we adopt
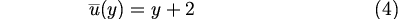
|
as the basic zonal flow (figure 1). In this basic flow, an inertially unstable region exists in the region of 0 ≤ y ≤ 1 (a red shaded area in figure 1). The calculational domain used in most cases is -2 ≤ y ≤ 3 as well as TI2006. In sections 5 and 6, cases in which calculational domains are gradually expanded northward and/or southward are considered. The eigenvalue equations (1)-(3) are solved by discretizing in the y-direction with the grid interval 0.078125. The zonal wavenumber in the range of 0.00 ≤ k ≤ 1.00 is considered. Values of E within the range of -2.50 ≤ log E ≤ 7.50 are considered. |
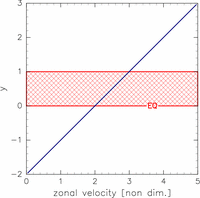
Figure 1: Meridional profile of the basic zonal wind.
Horizontal and vertical axes are velocity
|