大気や海洋の赤道域では 様々な不安定モードが発生すると議論されてきた. Dunkerton (1981) とStevens (1983) は, 赤道β平面浅水波モデルを用いて, ポテンシャル渦度とコリオリパラメータの積が負となる領域 (以下では, 慣性不安定領域と呼ぶ) が存在する場合には, 東西対称な構造を持つ慣性不安定モードが 発生することを示した. それ以外にも, 慣性不安定領域において発達する東西非対称な不安定モード (Dunkerton, 1983), 赤道ケルビン波 (Matsuno, 1966) が不安定化したモード (Natarov and Boyd, 2001) などが求められてきた.
Taniguchi and Ishiwatari (2006, 以降 TI2006)
は中立波の共鳴の理論
(Hayashi and Young, 1987;
Iga, 1999c)
から,これらの不安定モードの再解釈を行った.
彼らは, 無次元パラメータ
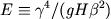を変化させて,
赤道β平面浅水系の線形シアー流中に生じる不安定モードを
固有値計算によって求めた.
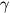は基本場の南北シアー,
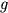は重力加速度,
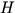は等価深度,
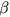はコリオリパラメータの南北勾配である.
TI2006 は E の値に応じて 最大不安定モードをもたらす 中立波の組を表 1 に示すように整理した (図に示していない E の値における 分散曲線についてはアニメーション を参照されたい). これにより, Dunkerton (1983) の東西非対称不安定モードと, Dunkerton (1981) および Stevens (1983) によって議論された 東西対称構造を持ついわゆる慣性不安定モードは, 赤道ケルビン波モードと西進混合ロスビー重力波モード (Matsuno, 1966) の共鳴によって もたらされる同種の不安定モード であることを示した. また, Natarov and Boyd (2001) によって求められた 不安定化した赤道ケルビン波は, 赤道ケルビン波モードと連続モード (Case, 1960) の共鳴によってもたらされる 不安定モードに対応していることが示された.
| log E の範囲 | log E < 1.00 | 1.00 < log E < 2.00 | log E > 2.00 |
| 分散曲線図 |
|
|
 |
| 構造 | 東西非対称構造 | 東西非対称構造 |
東西対称構造 |
| 共鳴の組 | 赤道ケルビン波モードと連続モード |
赤道ケルビン波モードと 西進混合ロスビー重力波モード |
赤道ケルビン波モードと 西進混合ロスビー重力波モード |
| 対応する過去の研究 |
Natarov and Boyd (2001) の不安定化した 赤道ケルビン波 |
Dunkerton (1983) の東西非対称モード |
Dunkerton (1981), Stevens (1983)の 慣性不安定モード |
表1: TI2006 で得られた最大不安定モードの解釈のまとめ. (a) log E=-0.90, (b) log E=+1.30, (c) log E=+2.50 の場合を示す. 上段は, それぞれの E の値における分散曲線図. 分散曲線図をクリックするとそれぞれの拡大した図を見ることができる. 横軸は無次元波数, 縦軸は位相速度 c. 図中の "Kelvin", "E-MRG", "W-MRG", "Eastward Gravity", "Westward Gravity" のラベルは, それぞれ赤道ケルビン波モード, 東進混合ロスビー重力波モード, 西進混合ロスビー重力波モード, 東進慣性重力波モード, 西進慣性重力波モード を示す(それぞれのモードについては, Matsuno (1966) を参照されたい). "Kelvin + W-MRG" のラベルは, 赤道ケルビン波モードと西進混合 ロスビー重力波モードとの共鳴による不安定モードを示す. 0.00 < c < 5.00 の領域の水平の直線群は, 連続モードの分散曲線である. 赤◯印は不安定モード, 青◎印はその log E での最大不 安定モードを示す. △, ▲印はそれぞれ北側, 南側の境界ケルビン波モードの分散曲線の位置を示す. 三段目, 四段目はそれぞれ最大不安定モードの水平構造の特徴, 共鳴を起こす中立波の組み合せを示す. 最下段は, それぞれの最大不安定モードと対応する過去の研究で得られた解 を示す.
