Next: A.2 鉛直方向の離散化にルジャンドル多項式を用いる理由 Up: A 計算の詳細について Previous: A 計算の詳細について
![]() における基本場
における基本場![]() を運動方程式に代入すると
を運動方程式に代入すると
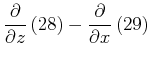 より
より
そこで、運動方程式を以下のように修正し、基本場のsin型シア流を維持する。
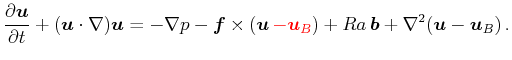 |
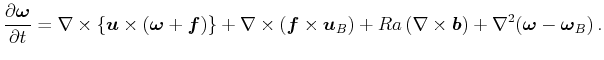 |
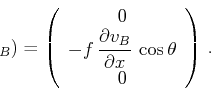 |
Hathaway & Somerville(1987)[2]でも、ジェットを維持する強制として「ジェットに働くコリオリ力・粘性力と釣り合う応力」を与えており、これに対応する修正を行ったことになる。
ちなみに、Hathaway & Somerville(1987)[2]ではこの応力のソースは規定せず、「柱状対流、傾圧過程、2次元乱流カスケード、平均子午面循環によって生み出される」としている。
SAITO Naoaki