Next: A.3 ルジャンドル多項式 Up: A 計算の詳細について Previous: A.1 基本場の維持について
回転軸の方向が鉛直な場合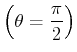 は、鉛直方向の離散化にsin,cos級数展開を用いたが(齊藤 & 石岡(2008)[5])、回転軸が傾いた場合
は、鉛直方向の離散化にsin,cos級数展開を用いたが(齊藤 & 石岡(2008)[5])、回転軸が傾いた場合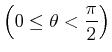 はルジャンドル多項式展開を用いる必要がある。
はルジャンドル多項式展開を用いる必要がある。
sin, cos級数展開では、鉛直方向の境界条件により2通りの展開を行う。
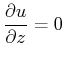 at at |
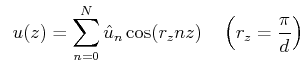 |
||
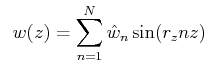 |
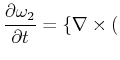 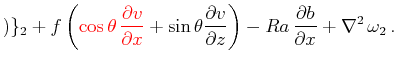 |
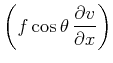 だけがcos型であり、その他の項は全てsin型である。このような不整合がある場合、このまま計算を行う事も可能だが、計算精度の低下は避けられない。これは、sin級数展開を行うことにより、あらゆる偶数階微分がゼロとなるという余計な境界条件を課してしまうため、その条件に適合しない問題の場合にはsin級数展開による収束が非常に遅くなってしまうからである。
だけがcos型であり、その他の項は全てsin型である。このような不整合がある場合、このまま計算を行う事も可能だが、計算精度の低下は避けられない。これは、sin級数展開を行うことにより、あらゆる偶数階微分がゼロとなるという余計な境界条件を課してしまうため、その条件に適合しない問題の場合にはsin級数展開による収束が非常に遅くなってしまうからである。
よって、十分な計算精度を確保するため、回転軸が傾いた場合では鉛直方向の離散化にルジャンドル多項式展開を用いる。
SAITO Naoaki