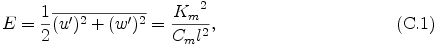
| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |
The effects of subgrid scale turbulence are implemented using the parameterization of Klemp and Wilhelmson (1978) [1]. In this parameterization, turbulent mixing coefficients are diagnosed from the turbulent kinetic energy that is predicted by a prognostic equation.
The turbulent mixing coefficient for momentum Km is diagnosed from the turbulent kinetic energy E.
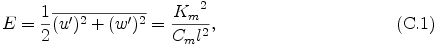
where Cm = 0.2, l = (Δ x Δ z)1/2. Δ x, Δ z are grid intervals in the x and z directions, respectively. By using eq. (C.1), the prognostic equation of the turbulent kinetic energy E can be expressed in terms of the turbulent mixing coefficient for momentum.
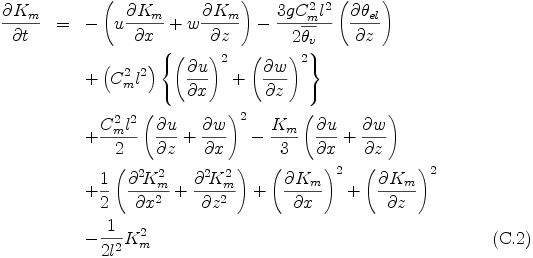
where
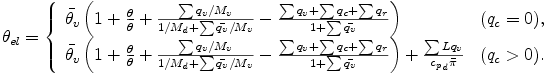
For the sake of numerical stability, the value of Km is assumed to be bounded, and its maximum value is set to 800 m2s-1 [6].
The turbulent momentum mixing terms in eq. (A.4) and eq. (A.5) are now given by
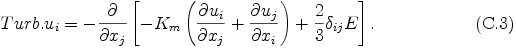
The turbulent mixing terms in eq. (A.7) and eq. (A.8) are given by
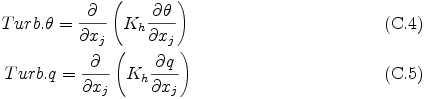
where Kh is the turbulent mixing coefficient for scalar variables that is estimated from Km by the following relationship,
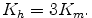
Heating due to dissipation in eq. (A.7) is given by

where Cε = Cm = 0.2.
| Development of a Numerical Model for Jupiter's Atmosphere | << Prev | Index| Next >> |