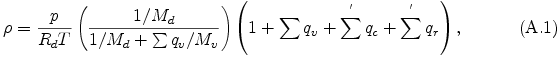
| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |
The dynamic framework of the model is based on the quasi-compressible system [1]. In this framework, each variables is divided into horizontally uniform basic state and residual perturbation, and prognostic equations of residual perturbations are solved.
Derivation of the momentum and pressure equations requires use of the equation of state that includes the effects of condensible species.
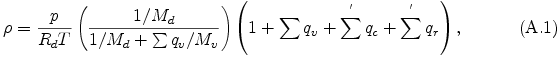
where ρ is density of moist air, p is pressure, Rd is the gas constant for dry air per unit mass, T is temperature, and Md and Mv are molecular weights of non-condensible and condensible components, respectively. qv is the mixing ratio of each condensible volatiles, and qc and qr are cloud and rain mixing ratio of each condensed species, respectively. ∑ and ∑' represent the summation for condensible volatiles and condensed species, respectively. By using eq. (A.1), the exner function π is written in the form:
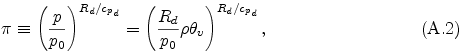
where p0 is the base state pressure, cpd is specific heat of dry air, and θv is the virtual potential temperature defined by
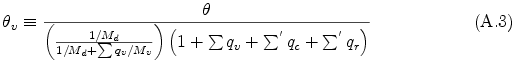
and potential temperature θ is defined as θ = T / π.
This dynamical framework ignores the dependences of mean specific heat on temperature and composition, since potential temperature is utilized. However, the value of static stability N2, which governs the gross structure of convection layer, is almost the same as that obtained when the dependences ignored above are taken into consideration (see Appendix G).
The momentum equations are expressed in the following forms:
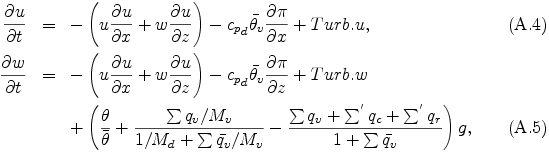
where u is velocity in x direction, w is velocity in z direction, g is the acceleration due to gravity, and Turb.u and Turb.w refer to subgrid scale turbulent momentum mixing described in Appendix C. The variables denoted with over bar - represent horizontally uniform basic state.
The pressure equation is derived by using the compressible continuity equation
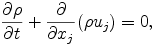
eq. (A.1)--(A.3) , and the thermodynamic equation (A.7), which will be described later.
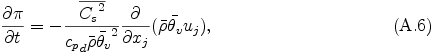
where Cs is the phase velocity of sound wave given by Cs2 = cpd Rdπ &thetav / cvd. The terms which correspond to pressure variation caused by diabatic heating are neglected following Klemp and Wilhelmson (1978) [1].
The thermodynamic equation can be written in the form:
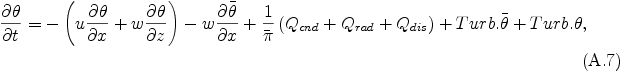
where Qcnd refers to heating by condensation described in Appendix B, Qrad refers to radiation heating, and Qdis and Turb.θ refer to dissipative heating and subgrid scale turbulent mixing of potential temperature which are described in Appendix C, respectively.
The conservation equations for condensible species can be written in the form:
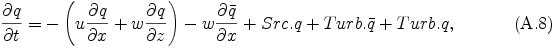
where Src.q refers to source terms described in Appendix B and Turb.q refers to subgrid scale turbulent mixing terms described in Appendix C.
| Development of a Numerical Model for Jupiter's Atmosphere | << Prev | Index| Next >> |