| Development of a Cloud Convection Model for Jupiter's Atmosphere | << Prev | Index| Next >> |
The microphysical processes represented by Qcnd in eq. (A.7) and Src in eq. (A.8) are implemented using the warm rain bulk parameterization of Kessler (1969) [2]. In this parameterization scheme, each condensible species is divided into three categories ``vapor'', ``cloud'', and ``rain''; both rain and cloud are condensed phases, but rain falls down relative to the air, whereas cloud does not (see Fig. 2.1). The conversion rates between each pair of categories are calculated using bulk mixing ratios of the three categories of condensible components. For simplicity, we assume that the condensed phase consists of pure condensible species; solution is not considered. Moreover, we assume that the interactions between the three condensed materials, i.e. H2O ice, NH4SH ice, and NH4SH ice, are absent.
The condensation heat Qcnd in eq. (A.7) is expressed as
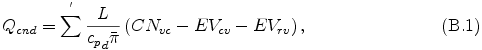
where L is latent heat or reaction heat, CNvc is conversion rate from vapor to cloud due to condensation or reaction, EVcv is conversion rate from cloud to vapor due to evaporation, and EVrv conversion rate from rain to vapor due to evaporation. The source term in eq. (A.8) for "vapor", "cloud", and "rain" are expressed by the following equations.
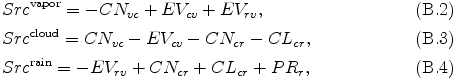
where CNcr is conversion rate from cloud to rain due to autoconversion, CLcr is conversion rate from cloud to rain due to collection of cloud by rain. By substituting eqs. (B.1) -- (B.4) into eq. (A.7) and eq. (A.8), eq. (A.7) and eq. (A.8) may be rewritten as the follows:
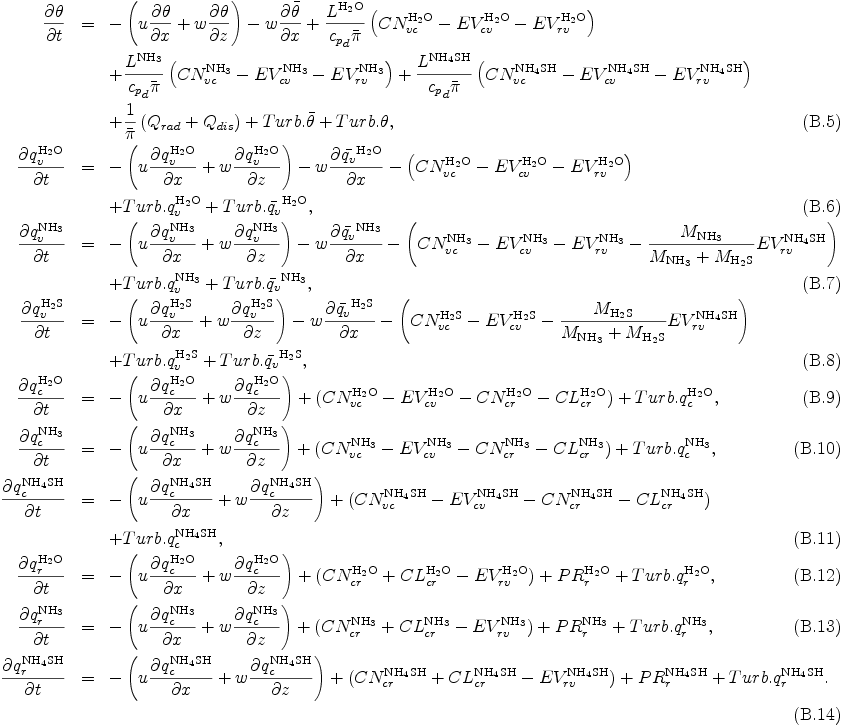
The terms in eqs. (B.5)--(B.14) associated with cloud microphysical processes are given in the following subsection.
The conversion rate from cloud to rain due to autoconversion is determined by the following equation.

The time constant of autoconversion τ0 is 100 sec, and the threshold cloud mixing ratio q0 is set to zero, following Nakajima et al. (2000) [6]. These values have been selected by roughly taking into account the effects of the larger terminal velocity of Jupiter's precipitation [15].
The conversion rate from cloud to rain due to collection of cloud by rain is determined by the following equation.

where fj is ratio of Jupiter and Earth's gravitational acceleration, and fj = 3 is adopted [6], [15].
The conversion rate from rain to vapor due to evaporation is given as proportional to the amount of supersaturation qvsw - qv .
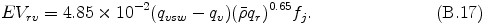
The tendency of rain due to precipitation is calculated by the following equation.

where the terminal velocity of rain, Ur [m s-1], is given by

Condensation and evaporation between vapor and cloud are evaluated by adjusting θ, qv, and qc to the saturated state, if necessary and possible, after eqs. (B.5)--(B.14) are integrated without - CNvc + EVcv, following Klemp and Wilhelmson (1978) [1].
In the followings, we denote the variables calculated from the integration of eqs. (A.4)--(A.8) and eqs. (B.5)--(B.14) without - CNvc + EVcv with an asterisk, θ*, qv*, and qc*, and variables after adjustment by θ, qv, and qc.
From the first low of thermodynamics, the following relationship between the quantities before and after the adjustment holds.
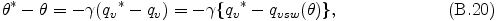
where qvsw is saturation vapor mixing ratio and qv = qvsw is assumed, and γ is equal to Lv/cpdπ. qvsw is calculated from the H2O or NH3 saturation vapor pressure and latent heat shown in Appendix F . By the Taylor expansion of qvsw around θ*, neglecting the terms higher than the 2nd order of (θ* - θ), eq. (B.20) is approximated to the following relation.
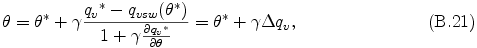
where
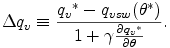
From eq. (B.21), the amount of condensation CNvc and evaporation EVcv are represented by
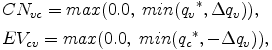
because the mixing ratios of variables after adjustment should be non-negative, and CNvc and EVcv are defined as positive variables.
Finally, θ, qv, and qc are determined by the following equations.
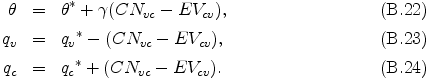
The above procedure is repeated four times to ensure the precision of the saturated state.
The partial pressures of NH3 and H2S have to satisfy the equilibrium condition of the NH4SH production reaction, NH3 + H2S ↔ NH4SH. The equilibrium constant is given by

where pNH3 and pH2S are partial pressures of NH3 and H2S, respectively (details on Kp are given in Appendix F. Eq. (B.25) is rewritten by using the change of partial pressure Δ pNH4SH required for the production of NH4SH.
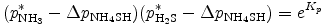
or
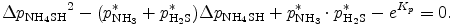
By solving this equation, we can obtain Δ pNH4SH as
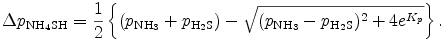
Note that the minus sign of square root is selected by ensuring Δ qNH4SH < pH2S and Δ qNH4SH < pH2S. Now we have CNvc and EVcv as
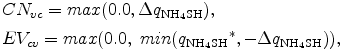
because the mixing ratios of variables after adjustment should be non-negative, and CNvc and EVcv are defined as positive variables. Δ qNH4SH is calculated from Δ pNH4SH.
Finally, θ, qNH3, qH2S, and qNH4SH are determined by the following equations.
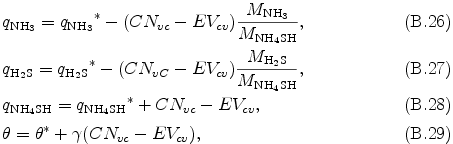
where MNH3, MH2S, and MNH4SH are molecular weights of NH3, H2S, and NH4SH, respectively. The above procedure is repeated four times to ensure the precision of the equilibrium state.
| Development of a Numerical Model for Jupiter's Atmosphere | << Prev | Index| Next >> |