|
Development of a Cloud Convection Model for Jupiter's Atmosphere
|
<< Prev |
Index|
Next >>
|
The basic equations of the model are based on the quasi-compressible system
[1]
and conservation
equations of condensible species. For the purpose of facilitating the
large horizontal-scale calculations, the model presented here
is two-dimensional (2D)
in the horizontal and vertical directions only.
The details of the dynamic framework are shown in Appendix
A.
The numerical code based on this system is,
compared to that based on anelastic system employed by
Nakajima et al. (2000)
[6],
more suitable for
large-scale calculation on parallel computers using domain
separation, and therefore more suitable for
modification from 2D to 3D model,
since there is no need to solve
elliptic differential equations.
The quasi-compressible system is also a useful approximate system which,
compared to the full-compressible system,
can suppress the increase of computational cost
[8]
by substituting the value of sound wave speed to that for
the basic reference state.
These are the reasons why
the quasi-compressible system is often utilized in recent
cloud convection models of the Earth's atmosphere.
The model atmosphere consists of H2, He,
H2O, NH3, and H2S.
The atmosphere is supposed to follow the equation of state of ideal gas.
H2 and He are treated as dry (non-condensible)
components while H2O, NH3, and
H2S are considered as condensible components, and the
following condensations and reaction are considered.
- H2O(g) ↔ H2O(s)
- NH3(g) ↔ NH3(s)
- H2S(g) + NH3(g) ↔ NH4SH(s)
The latent and reaction heats are considered in the thermodynamic
equation. Each condensed phase species is divided into two categories,
``cloud'' and ``rain''; rain falls down relative to the air, whereas
cloud does not. For simplicity, we assume that the condensed phases of
cloud and rain consist of pure condensible species; solution is not
considered.
The conversion between the categories is implemented by bulk
parameterization scheme of
Kessler (1969) [2]
used widely
in the modeling studies on terrestrial cloud convection.
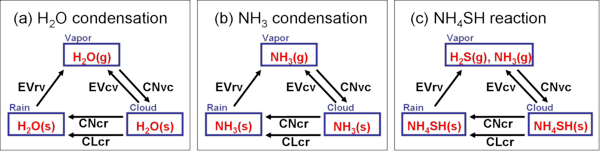
This parameterization scheme evaluates conversion rates between vapor,
cloud, and rain by considering the cloud microphysical processes shown
in Fig. 2.1.
This parameterization is considered
to be suited for "warm rain" which does
not involve solid phase clouds.
It is unclear to what extent the parameterization is approriate to the
actual atmosphere of Jupiter, where liquid and solid phase clouds may
possibly coexist.
In this study, as a starting point, we employ the scheme of
Kessler (1969) [2],
selected for its simplicity and wide usage.
The details are given in Appendix B.
|
|
Figure 2.1:
Cloud microphysical processes considered in the model.
CNvc represents condensation or reaction from vapor to cloud;
EVcv, evaporation from cloud to vapor;
EVrv, evaporation from rain to vapor;
CNcr, autoconversion from cloud to rain;
and CLcr, collection from cloud to rain.
See Appendix B for details.
|
The effect of subgrid scale turbulence is implemented using the
parameterization scheme of
Klemp and Wilhelmson (1978) [1].
The turbulent mixing coefficients are diagnosed from
the turbulent kinetic energy that is predicted by a prognostic
equation. The details are shown in Appendix C.
|
Development of a Cloud Convection Model for Jupiter's Atmosphere
|
<< Prev |
Index|
Next >>
|
