木星雲対流モデルの開発 << Prev | Index| Next >>

C. 乱流混合のパラメタリゼーション

モデル格子間隔以下のスケールを持つ乱流による拡散の効果は, Klemp and Wilhelmson (1978) [1] のパラメタリゼーションにしたがって計算する. このパラメタリゼーションでは, 乱流拡散係数をモデル格子間隔以下のスケールの乱流の運動エネルギーの予報方程式を解くことでを求める.

乱流運動エネルギーと運動量乱流拡散係数

乱流拡散係数 Km は 乱流運動エネルギー E より診断的に求まる.

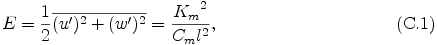
ここで Cm = 0.2, l = (Δ x Δ z)1/2, Δ x, Δ z はそれぞれ x, z 方向の格子間隔である. (C.1) 式を用いることで, 乱流運動エネルギー E の時間発展方程式は乱流拡散係数 Km の時間発展方程式として表現することができる.

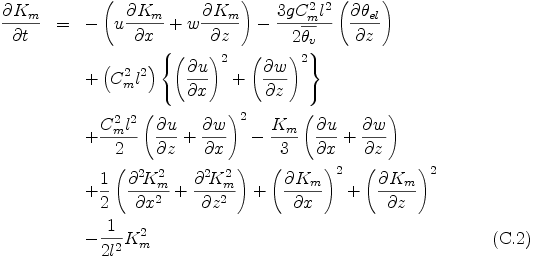
ここで,

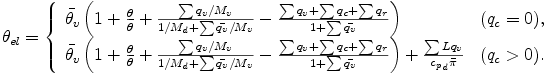
数値計算の安定性を確保するため, Km の上限値を設定し, その値を 800 m2s-1 とする [6].

乱流拡散項の表現

(A.4) 式と (A.5) 式中の乱流拡散項は以下のように与える.

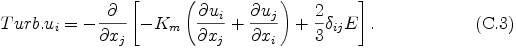
(A.7) 式と (A.8) 式中の乱流拡散項は以下のように与える.

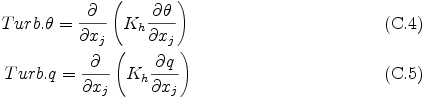
ここで Kh は スカラー量の乱流拡散係数であり, 以下の関係式を用いて Km より求める.

熱力学の式の散逸加熱項

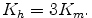
式 (A.7) 中の散逸加熱項は以下のように与える.

ここで Cε = Cm = 0.2 とする.

木星雲対流モデルの開発 << Prev | Index| Next >>